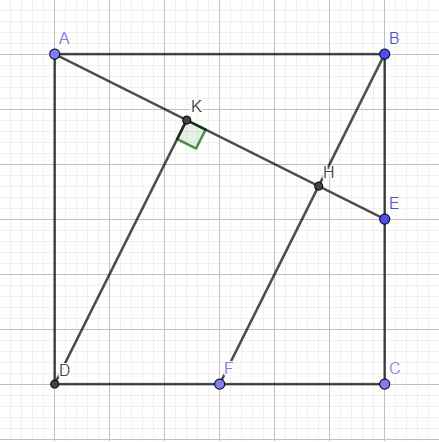
Cho hình vuông ABCD,gọi E,F lần lượt là trung điểm của BC,CD ; H là giao của AE,BF. . TínhAH/AE , BH/BF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


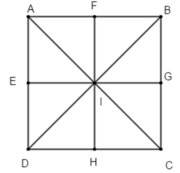
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H.
Chọn đáp án C

a. Dễ dàng chứng minh hai tam giác vuông ABE và BCF bằng nhau (c.g.c)
\(\Rightarrow\widehat{AEB}=\widehat{BFC}\)
Mà \(\widehat{AEB}+\widehat{AEC}=180^0\Rightarrow\widehat{BFC}+\widehat{AEC}=180^0\)
\(\Rightarrow\widehat{EHF}=360^0-\left(\widehat{C}+\widehat{BFC}+\widehat{AED}\right)=90^0\)
Hay \(AE\perp BF\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ABE:
\(AB^2=AH.AE\Rightarrow AH=\dfrac{AB^2}{AE}\Rightarrow\dfrac{AH}{AE}=\dfrac{AB^2}{AE^2}=\dfrac{AB^2}{AB^2+BE^2}=\dfrac{AB^2}{AB^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{4}{5}\)
\(\dfrac{BH}{BF}=\dfrac{BH}{AE}=\dfrac{\dfrac{AB.BE}{AE}}{AE}=\dfrac{AB.BE}{AE^2}=\dfrac{AB.\dfrac{1}{2}AB}{AB^2+\left(\dfrac{1}{2}AB\right)^2}=\dfrac{2}{5}\)
c. Hai tam giác vuông ABH và DAK đồng dạng (\(\widehat{ADK}\) và \(\widehat{BAH}\) cùng phụ \(\widehat{DAK}\))
\(\Rightarrow\dfrac{AK}{AD}=\dfrac{BH}{AB}\Rightarrow AK=\dfrac{AD.BH}{AB}=BH\)
Mà \(tan\widehat{BAH}=\dfrac{BH}{AH}=\dfrac{BE}{AB}=\dfrac{1}{2}\Rightarrow BH=\dfrac{1}{2}AH\)
\(\Rightarrow AK=\dfrac{1}{2}AH\) hay K là trung điểm AH

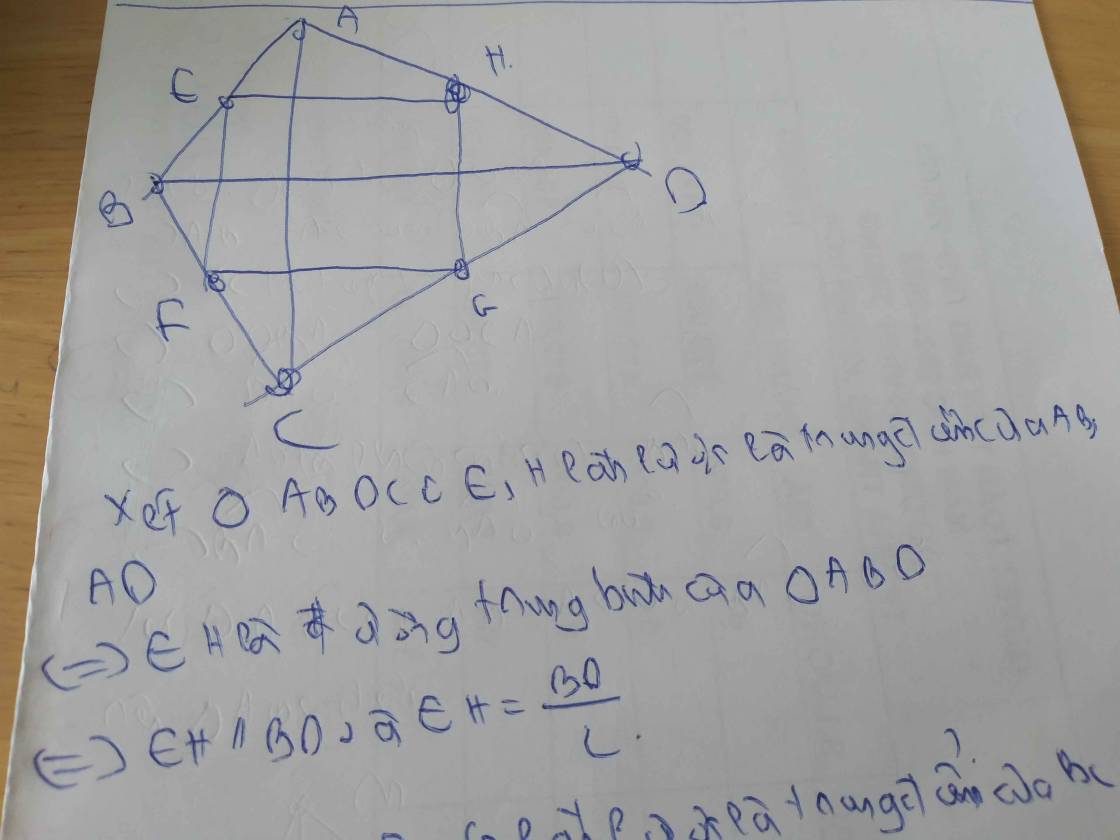
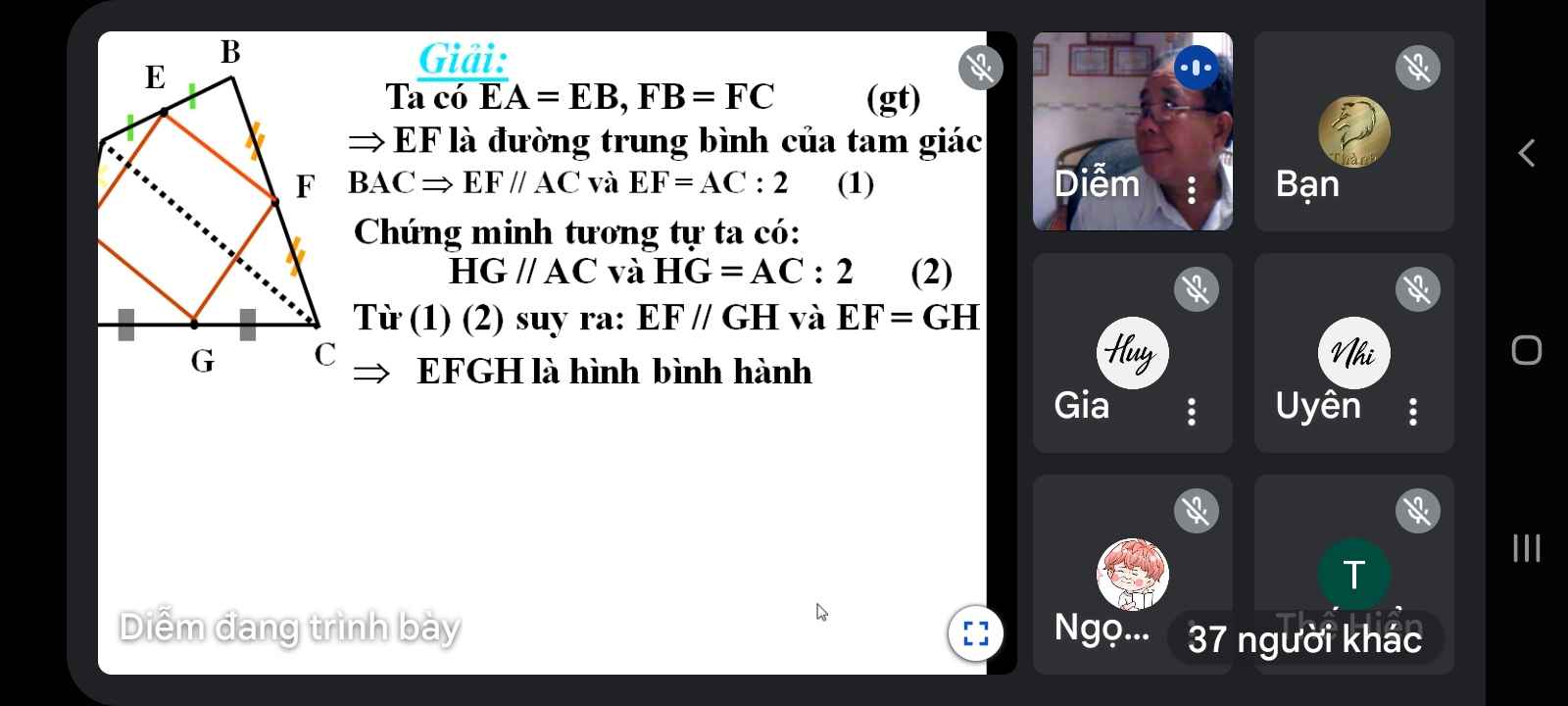
a: Xét ΔBAC có E,F lần lượt là trung điểm của BA,BC
=>EF là đường trung bình
=>EF//AC và EF=AC/2
Xét ΔDAC có
H,G lần lượt là trung điểm của DA,DC
=>HG là đường trung bình
=>HG//AC và HG=AC/2
=>EF//HG và EF=HG
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH=BD/2
=>EH=AC/2=EF
Xét tứ giác EHGF có
EF//GH
EF=GH
EH=EF
Do đó: EHGF là hình thoi
b: Xét ΔEHF có Q,M lần lượt là trung điểm của EH,EF
=>QM là đường trung bình
=>QM//HF và QM=HF/2
Xét ΔGHF có
P,N lần lượt là trung điểm của GH,GF
=>PN là đường trung bình
=>PN//HF và PN=HF/2
=>QM//PN và QM=PN
Xét ΔHEG có HQ/HE=HP/HQ=1/2
nên PQ//EG
=>PQ vuông góc HF
=>PQ vuông góc QM
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc PQM=90 độ
Do đó: MNPQ là hình chữ nhật