Cho a > b > 0 thỏa mãn3a2 +3b2 = 10ab.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MM
0
NL
0
ND
1
6 tháng 9 2017
Xét: P2 = \(\dfrac{\left(a-b\right)^2}{\left(a+b\right)^2}=\dfrac{a^2-2ab+b^2}{a^2+2ab+b^2}=\dfrac{3a^2+3b^2-6ab}{3a^2+3b^2+6ab}=\dfrac{10ab-6ab}{10ab+6ab}=\dfrac{4ab}{16ab}=\dfrac{1}{4}\)
=> P = \(\dfrac{1}{2}\)
5 tháng 5 2016
Xét \(3a^2+3b^2=10ab\Rightarrow a^2+b^2=\frac{10ab}{3}\)
hay: \(a^2+b^2=\frac{10}{3}ab\Rightarrow a^2+b^2+2ab=\frac{10}{3}ab+2ab\Rightarrow\left(a+b\right)^2=\frac{16}{3}ab\) (1)
\(a^2+b^2=\frac{10}{3}ab\Rightarrow a^2+b^2-2ab=\frac{10}{3}ab-2ab\Rightarrow\left(a-b\right)^2=\frac{4}{3}ab\) (2)
Ta có \(p=\frac{a+b}{a-b}\Rightarrow p^2=\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\frac{\frac{16}{3}ab}{\frac{4}{3}ab}=4\) Vậy \(p=2\) hoặc \(p=-2\)
6 tháng 5 2016
ta có 3a^2 +3b^2=10ab
<=> 3a(a-3b) - b(a-3b)=0
<=> (3a-b)(a-3b)=0
=> a=3b ; 3a=b (loại vì a>b>0)
thay a=3b
ta có P=3b-b/3a+b
= 2b/4b
=1/2
13 tháng 7 2017
\(3a^2+3b^2=10ab\)
\(\Rightarrow3a^2-10ab+3b^2=0\)
\(\Rightarrow3a^2-9ab-ab+3b^2=0\)
\(\Rightarrow3a\left(a-3b\right)-b\left(a-3b\right)=0\)
\(\Rightarrow\left(3a-b\right)\left(a-3b\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3a-b=0\\a-3b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3a=b\\a=3b\end{matrix}\right.\)
\(a>b>0\)
\(\Rightarrow a=3b\)
Thay vào biểu thức ta có:
\(\dfrac{a-b}{a+b}=\dfrac{3b-b}{3b+b}=\dfrac{2b}{4b}=\dfrac{1}{2}\)
23 tháng 5 2018
Ta có :
3a2 + 3b2 = 10ab
<=> 3a2 + 3b2 - 10ab = 0
<=>4a2 - a2 + 4b2 - b2 - 8ab- 2ab = 0
<=> ( 4a2 - 8ab + 4b2 ) - ( a2 + 2ab + b2 ) = 0
<=> ( 2a + 2b )2 - ( a - b )2 = 0
<=> ( 2a + 2b )2 = ( a - b )2
<=> 2a + 2b = a - b ( 1 )
Thay (1) vào P ta được :
\(P=\frac{2a+2b}{a+b}\)
\(P=\frac{2\left(a+b\right)}{a+b}\)
\(P=2\)
23 tháng 5 2018
Mạo danh cũng ko xong , chúa pain ko bao giờ nói " giúp pain đi " hay đúng hơn là t ko cần con người giải giúp mấy bài toán easy ntn này
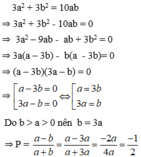
\(3a^2+3b^2=10ab\)
\(3a^2+3b^2-10ab=0\)
\(3\left(\frac{a}{b}\right)^2-\frac{10a}{b}+3=0\)
đặt \(\frac{a}{b}=x\)
\(3x^2-10x+3=0\)
\(3x^2-9x-1x+3=0\)
\(3x\left(x-3\right)-\left(x-3\right)=0\)
\(\left(3x-1\right)\left(x-3\right)=0\)
\(\orbr{\begin{cases}x=\frac{1}{3}\\x=3\end{cases}}\)
\(TH:x=3:\frac{a}{b}=3\)
\(a=3b\)
xét \(ĐKXĐ:a>b>0\)
\(< =>a=3b\left(KTM\right)\)
\(TH2:x=\frac{1}{3}< =>\frac{a}{b}=\frac{1}{3}\)
\(3a=b\left(TM\right)\)
vậy \(a=1;b=3\)