Tìm m để phương trình x^4−2x^2+m−2=0 có 4 nghiệm phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QH
1
22 tháng 7 2017
Tìm m để Phương trình: x4-2x2-m=0 có 4 nghiệm phân biệt.
Đặt t=x2=>t>=0
Phương trình trở thành: t2-2t-m=0 (*)
Để phương trình đã cho có 4 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương:
Do đó nó phải thỏa 3 điều kiện sau:
<=>
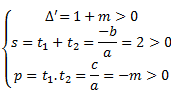
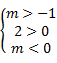
Vậy -1<m<0
mik nha
QH
5
SL
23 tháng 5 2017
Đặt x^2=a ,,, để phương trình có 4 nghiệm thì phương trình đặt phải có 2 nghiệm dương phân biệt
PN
18 tháng 4 2022
Đặt \(x^2=a\left(a\ge0\right)\)khi đó phương trình tương đương với
\(a^2-5a+m=0\)(*)
Để phương trình có 4 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt dương
\(< =>\left\{{}\begin{matrix}\Delta>0\\x_1.x_2>0\\x_1+x_2>0\end{matrix}\right.< =>\left\{{}\begin{matrix}25-4m>0\\m>0\\5>0\end{matrix}\right.\)
\(< =>\dfrac{25}{4}>m>0\)