Cho hình thang ABCD (AB//CD). giả sử rằng AC = BD. Chứng minh rằng ABCD là 1 hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2022
Câu 1:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
Suy ra: DE=CF
Bài 2:
b: Xét ΔBAD và ΔABC có
AB chung
AD=BC
BD=AC
Do đó: ΔBAD=ΔABC
Suy ra: góc EAB=góc EBA
=>ΔEAB cân tại E
=>EA=EB
2 tháng 9 2021
Bài 1:
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Suy ra: \(\widehat{BAC}=\widehat{ABD}\)
hay \(\widehat{EAB}=\widehat{EBA}\)
hay ΔEAB cân tại E
25 tháng 8 2019
A B C D O
Xét tam giác ABC và BAD có :
AB : chung
\(\widehat{BAD}=\widehat{ABC}\)
AD = BC
( ABCD là hình thang cân )
\(\Rightarrow\Delta ABC=\Delta BAD\)
\(\Rightarrow\widehat{BAC}=\widehat{ABD}\)
\(\Delta AOB\)CÓ : \(\widehat{OAB}=\widehat{OBA}\Rightarrow\Delta AOB\)cân tại O nên OA = OB
M
22 tháng 9 2016
cho mình xin lỗi ,câu c mình ghi sai 1 câu nhưng ko quan trọng lắm
"hình bình hành có 2 cạnh kề bằng nhau là hình thoi,bạn xem lại nhan,do mình bấm vội nhưng giải đúng đó
M
22 tháng 9 2016
bạn ghi đề sai rồi ,phải là AB=BC=AD và CD=2AB nhan
hình bạn tự vẽ đi nhan
câu a:ta có AB//CD(vì ABCD là hình thang) nên góc BDC=góc ABD(1)
lại có AD=AB(gt)nên tamgiacs ADB cân tại A nên góc ABD=góc ADB(2)
từ (1) và (2) ta có góc ADB =góc BDC nên BD là phân giác goc ADC
câu b:xét tam giác ADC và tam giác BDC ,có
AD=BC(gt);DC :chung và góc D=góc C(vì ABCD là hình thang cân) nên 2 tam giác này bằng nhau nên AC=BD
câu c:gọi K là trung điểm CD ,ta có AB=1/2 CD =CK,mà AB=BC(gt)nên BC=CK(3)
lại có AB=1/2CD=DK mà AB//DK(vì ABCD là hình thang) nên ABKD là hình bình hành
mặt khác AB=AD(gt) nên ABKD là hình thoi(vì hình bình nhành có 2 cạnh bên bằng nhau là hình thoi đó)
=>BK=AB mà BC=AB =>BK=BC(4)
từ (3)và (4)=>BK=BC=CK nên BCK là tam giác đều nên góc C=60 độ và bằng góc D,=> góc A=120độ và bằng góc B
XONG,MỎI TAY QUÁ BN K CHO MÌNH NHAN,BYE
2 tháng 9 2021
Bài 1:
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó:ΔABC=ΔBAD
Suy ra: \(\widehat{BAC}=\widehat{ABD}\)
hay \(\widehat{EAB}=\widehat{EBA}\)
hay ΔEAB cân tại E
CM
22 tháng 5 2017
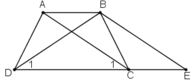
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
20 tháng 9 2019
A B C D E 1 1
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\) cân
b ) Ta có : AC // BE
\(\Rightarrow\widehat{C}_1=\widehat{E}\) ( 3 )
Tam giác BDE cân tại B ( câu a ) nên \(\widehat{D}_1=\widehat{E}\) ( 4 )
Từ (3 ) và ( 4 ) \(\Rightarrow\widehat{C}_1=\widehat{D}_1\)
Xét \(\Delta ACD\) và \(\Delta BCD\) có AC = CD ( gt )
\(\widehat{C}_1=\widehat{D}_1\left(cmt\right)\)
CD là cạnh chung
Nên \(\Delta ACD=\Delta BCD\left(c.g.c\right)\)
c ) Vì \(\Delta ACD=\Delta BCD\) ( câu b ) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Chúc bạn học tốt !!!
C
10 tháng 10 2020
1) Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau : Cho hình thang ABCD(AB//CD)ABCD(AB//CD) có AC=BDAC=BD. Qua BB kẻ đường thẳng song song với ACAC, cắt đường thẳng DCDC tại EE. Chứng minh rằng:
a) BDEBDE là tam giác cân.
b) △ACD=△BDC.△ACD=△BDC.
c) Hình thang ABCDABCD là hình thang cân.
chúc hok tốt , k nha! sai cũng k
Gọi giao điểm AC và BD là O
Có tam giác AOB đồng dạng với tam giác COD (g , g)
=> OC/AC = OD/BD
=> OC = OD
=> Tam giác OCD cân tại O
=> góc ACD = góc BDC (1)
Có: AC = BD, CD chung
=> tam giác ACD = tam giác BDC
=> góc ADC = góc BCD
=> tứ giác ABCD là hình thang cân