Bài 3 vs 4 ạ.cho mk lời giải chi tiết nha.tks
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
G4
1
Những câu hỏi liên quan
TG
2 tháng 7 2021
\(5x^2-10xy+5y^2-20z^2=5\left(x^2-2xy+y^2-4z^2\right)=5.\left[\left(x-y\right)^2-\left(2z\right)^2\right]=5.\left(x-y-2z\right).\left(x-y+2z\right)\)
\(x^2-z^2+y^2-2xy=\left(x-y\right)^2-z^2=\left(x-y+z\right)\left(x-y-z\right)\)
\(x^2-2xy-4z^2+y^2=\left(x-y\right)^2-4z^2=\left(x-y-2z\right)\left(x-y+2z\right)\)
2 tháng 7 2021
a) 5x2 - 10xy + 5y2
= 5 (x2 - 2xy + y2)
= 5 (x - y)2
b) x2 - z2 + y2 - 2xy
= (x2 + y2 - 2xy) - z2
= (x2 - 2xy + y2) - z2
= (x - y)2 - z2
= (x - y + z)(x - y - z)
c) x2 - 6xy - 25z2 : hinh nhu de bi sai , ban xem lai giup minh
d) x2 - 2xy - 4z2 + y2
= (x2 - 2xy + y2) - 4z2
= (x - y)2 - (2z)2
= (x - y + 2z)(x - y - 2z)
Chuc ban hoc tot
26 tháng 2 2023
câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)
SM
1
QN
1
22 tháng 1 2022
Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
DO đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
22 tháng 1 2022
Xin lỗi ạ. Nhưng mk cần bài 2 ạ , xin lỗi zì đã lm phiền
BD
6 tháng 7 2023
\(\dfrac{1}{3}+\dfrac{5}{6}\cdot\left(x-\dfrac{11}{5}\right)=\dfrac{3}{4}\)
\(\dfrac{5}{6}\cdot\left(x-\dfrac{11}{5}\right)=\dfrac{3}{4}-\dfrac{1}{3}\)
\(\dfrac{5}{6}\cdot\left(x-\dfrac{11}{5}\right)=\dfrac{5}{12}\)
\(x-\dfrac{11}{5}=\dfrac{5}{12}\cdot\dfrac{6}{5}\)
\(x-\dfrac{11}{5}=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}+\dfrac{11}{5}\)
\(x=\dfrac{27}{10}\)
6 tháng 7 2023
\(\dfrac{5}{6}\left(x-\dfrac{11}{5}\right)=\dfrac{3}{4}-\dfrac{1}{3}\)
\(\dfrac{5}{6}\left(x-\dfrac{11}{5}\right)=\dfrac{5}{12}\)
\(x-\dfrac{11}{5}=\dfrac{5}{12}:\dfrac{5}{6}\)
\(x-\dfrac{11}{5}=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}+\dfrac{11}{5}=\dfrac{27}{10}\)
HT
11 tháng 12 2016
A = 1 - 2 + 3 - 4 +...+ 43 - 44 + 45
=> A = (1 - 2) + (3 - 4) +....+ (43 - 44) + 45
=> A = -1 + (-1) +....+ (-1) + 45
=> A = (-1).22 + 45
=> A = -22 + 45
=> A = 23
11 tháng 12 2016
20 vì :
Khi - cộng thì 2 số có cùng một tích
Vậy thì ra thôi
1 tháng 7 2021
a) Ta có: \(x^2-y^2-2x+2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-2\right)\)
b) Ta có: \(2x+2y-x^2-xy\)
\(=2\left(x+y\right)-x\left(x+y\right)\)
\(=\left(x+y\right)\left(2-x\right)\)
c) Ta có: \(x^2-25+y^2+2xy\)
\(=\left(x+y\right)^2-25\)
\(=\left(x+y-5\right)\left(x+y+5\right)\)
d) Ta có: \(3x^2-6xy+3y^2-12z^2\)
\(=3\left(x^2-2xy+y^2-4z^2\right)\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)
e) Ta có: \(x^2+2xy+y^2-xz-yz\)
\(=\left(x+y\right)^2-z\left(x+y\right)\)
\(=\left(x+y\right)\left(x+y-z\right)\)
f) Ta có: \(x^2-2x-4y^2-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
QN
1
22 tháng 1 2022
Bài 8:
a: Xét ΔDAB vuông tại B và ΔDAC vuông tại C có
DA chung
AB=AC
Do đó: ΔDAB=ΔDAC
b: Ta có: ΔDAB=ΔDAC
nên DB=DC
hay ΔDBC cân tại D
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
ta có: MB=MC
nên M nằm trên đường trung trực của BC(2)
Ta có: DB=DC
nên D nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,M,D thẳng hàng
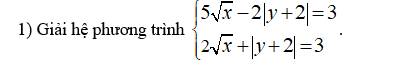
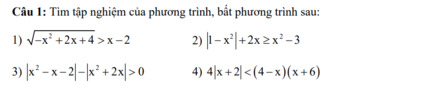
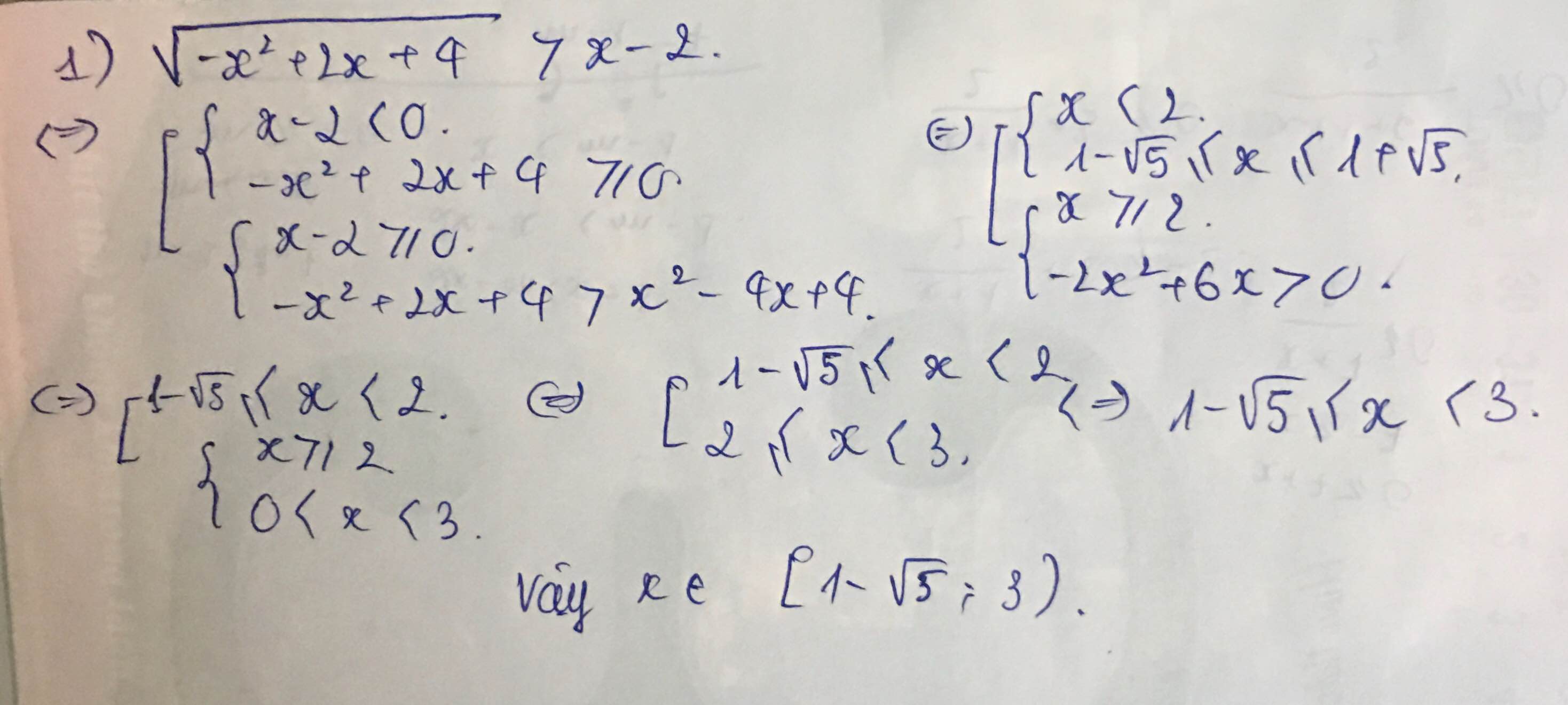
Khó nhỉ
Yeah