Tìm x và y, biết: 2x - 2y =256
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 4 2023
a.
$7x-2y=5x-3y$
$\Leftrightarrow 2x=-y$. Thay vào điều kiện số 2 ta có:
$-y+3y=20$
$2y=20$
$\Rightarrow y=10$.
$x=\frac{-y}{2}=\frac{-10}{2}=-5$
AH
Akai Haruma
Giáo viên
30 tháng 4 2023
b.
$2x=3y\Rightarrow \frac{x}{3}=\frac{y}{2}$
$3y=4z-2y\Rightarrow 5y=4z\Rightarrow \frac{y}{4}=\frac{z}{5}$
$\Rightarrow \frac{x}{6}=\frac{y}{4}=\frac{z}{5}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{6}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{6+4+5}=\frac{45}{15}=3$
$\Rightarrow x=6.3=18; y=4.3=12; z=5.3=15$
TT
26 tháng 11 2014
1) ADTCDTSBN, ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)= \(\frac{2x^2+2y^2-3z^2}{18+32-75}=\frac{-100}{-25}\)= 4
* \(\frac{x}{3}=4\)=> x = 3 . 4 = 12
- \(\frac{y}{4}=4\)=> y = 4 . 4 = 16
* \(\frac{z}{5}=4\)=> z = 5 . 4 = 20
Vậy x = 12
y = 16
z = 20
HN
1
NT
0
LP
0
15 tháng 9 2015
1. 2x = 3y-2
2x+2x = 3y
4x = 3y
=> \(\frac{x}{3}=\frac{y}{y}\Rightarrow\frac{x+y}{3+4}=\frac{14}{7}=2\)
=> \(\frac{x}{3}=2\Rightarrow x=6\)
=> \(\frac{y}{4}=2\Rightarrow y=8\)
PT
1
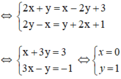
2x-2y=256
=>2y(2x-y-1)=256
vì 2x-y-1 không chia hết cho 2 mà 256 chia hết cho 2x-y-1
=>2x-y-1=1
=>2x-y=2
=>x-y=1
=>2y(21-1)=256
=>2y=28
=>y=8
=>x=9
vậy (x;y)=(9;8)
\(2^x-2^y=256\)
=> \(2^x-2^y=2^8\)=> \(2^y.\left(2^{x-y}-1\right)=2^8\) (1)
dễ thấy x \(\ne\)y , ta xét 2 trường hợp:
a) Nếu x - y = 1 thì từ (1) ta có \(2^y.\left(2-1\right)=2^8\)Suy ra y = 8 ; x = 9
b) Nếu x - y \(\ge2\)thì \(2^{m-n}-1\)là một số lẻ lớn hơn 1 nên vế trái của (1) chứa thừa số nguyên tố lẻ khi phân tích ra thừa số nguyên tố. Còn vế phải của (1) chỉ chứa thừa số nguyên tố 2. Mâu thuẫn.
Vậy y = 8 ; x = 9 là đáp án duy nhất.