Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Định lý 1
- Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.[1]
Đề bài minh hoạ:
Cho tam giác ABC có M là trung điểm cạnh AB. Đường thẳng đi qua M song song với cạnh BC và cắt cạnh AC tại điểm N. Chứng minh {\displaystyle NA=NC}
Chứng minh định lý:
Từ M vẽ tia song song với AC, cắt BC tại F. Tứ giác MNCF có hai cạnh MN và FC song song nhau nên là hình thang. Hình thang MNCF có hai cạnh bên song song nhau nên hai cạnh bên đó bằng nhau (theo tính chất hình thang): {\displaystyle MF=NC}
Xét hai tam giác BMF và MAN, có: {\displaystyle {\widehat {\rm {MBF}}}={\widehat {\rm {AMN}}}}




Từ (1) và (2) suy ra {\displaystyle NA=NC}
Định lý 2
Đường trung bình của tam giác thì song song với cạnh thứ ba và dài bằng nửa cạnh ấy.[2]
Cho tam giác ABC có M là trung điểm cạnh AB và N là trung điểm cạnh AC ({\displaystyle MA=MB}



Chứng minh định lý:
Kéo dài đoạn MN về phía N một đoạn NF có độ dài bằng MN. Nhận thấy: {\displaystyle \triangle ANM=\triangle CNF}
suy ra {\displaystyle {\widehat {\rm {MAN}}}={\widehat {\rm {NCF}}}}










D/L: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
ta lay vd 1 de bai de chung minh:
Cho tam giác ABC có M là trung điểm cạnh AB. Đường thẳng đi qua M song song với cạnh BC và cắt cạnh AC tại điểm N. Chứng minh {\displaystyle NA=NC}
ta chung minh dinh ly
Từ M vẽ tia song song với AC, cắt BC tại F. Tứ giác MNCF có hai cạnh MN và FC song song nhau nên là hình thang. Hình thang MNCF có hai cạnh bên song song nhau nên hai cạnh bên đó bằng nhau (theo tính chất hình thang): {\displaystyle MF=NC}
Xét hai tam giác BMF và MAN, có: {\displaystyle {\widehat {\rm {MBF}}}={\widehat {\rm {AMN}}}}




Từ (1) và (2) suy ra {\displaystyle NA=NC}
D/L : Đường trung bình của tam giác thì song song với cạnh thứ ba và dài bằng nửa cạnh ấy
VD : Cho tam giác ABC có M là trung điểm cạnh AB và N là trung điểm cạnh AC (


chung minh dinh li
Kéo dài đoạn MN về phía N một đoạn NF có độ dài bằng MN. Nhận thấy: {\displaystyle \triangle ANM=\triangle CNF}
suy ra {\displaystyle {\widehat {\rm {MAN}}}={\widehat {\rm {NCF}}}}










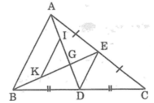
Có: `AD=DB => D` là trung điểm của `AB`.
Mà `K` là trung điểm của `BC`
`=> DK` là đường trung bình của `\DeltaABC`
`=> DK////AC ; DK=1/2 AC`
Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{1}{2}BC\)
Xét ΔABC có
D là trung điểm của AB
K là trung điểm của BC
Do đó: DK là đường trung bình của ΔABC
Suy ra: DK//AC và \(DK=\dfrac{AC}{2}\)

Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD

Cái Này Sẽ Được Chứng Minh Ở Bài Đường Trung Bình Lớp 8, Bạn Tra Mạng Sẽ Có Nhé!

Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2

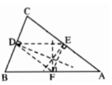
Gọi D là trung điểm của BC, E là trung điểm của AC. Theo câu a)) đường thẳng qua D, song song với AB phải cắt AC tại trung điểm của AC nên đường thẳng đó phải đi qua E, hay DE // AB.
M N A B C MN là đường trung bình của ABC P
\(\text{Trên tia đối của NM lấy P sao cho NM=NP}\)
\(\text{Do MN là đường trung bình của }\Delta ABC\left(gt\right)\Rightarrow M\text{ là trung điểm AB, N là trung điểm AC}\)
\(\Rightarrow AM=BM\left(\text{do M là trung điểm AB}\right),AN=CN\left(\text{ do N là trung điểm AC}\right)\)
\(\Delta ANM=\Delta CNP\text{ do}\hept{\begin{cases}NM=NP\\\widehat{ANM}=\widehat{CNP}\left(\text{đối đỉnh}\right)\\AN=CN\left(cmt\right)\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{AMN}=\widehat{CPN}\left(2\text{ góc tương ứng}\right)\\AM=CP\left(2\text{ cạnh tương ứng}\right)\end{cases}}\)
\(\text{Do }\widehat{AMN}=\widehat{CPN}\left(cmt\right),\text{mà 2 góc này ở vị trí so le trong của 2 đường thẳng AB và NP}\Rightarrow\text{AB//NP}\)\(\left(\text{dấu hiệu nhận biết}\right)\)
\(\Rightarrow\text{BM//NP}\left(do\text{ M}\in AB\right)\Rightarrow\widehat{BMC}=\widehat{PCM}\left(2\text{ góc so le trong}\right)\)
\(\text{Vì AM=CP(cmt), mà AM=BM(gt)}\Rightarrow BM=CP\)
\(\Delta BMC=\Delta PCM\text{ do}\hept{\begin{cases}BM=CP\left(cmt\right)\\\widehat{BMC}=\widehat{PCM}\left(\text{cmt}\right)\\MC\text{ chung}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{BCM}=\widehat{PMC}\left(2\text{ góc tương ứng}\right)\\BC=PM\left(2\text{ cạnh tương ứng}\right)\end{cases}}\)
\(\text{Ta có:}\widehat{BCM}=\widehat{PMC}\left(cmt\right),\text{mà 2 góc này ở vị trí so le trong của 2 đường thẳng MN và BC}\Rightarrow\text{MN//BC}\left(1\right)\)
\(PM=2.MN\Rightarrow MN=\frac{PM}{2},\text{ mà PM=BC}\Rightarrow MN=\frac{BC}{2}\left(2\right)\)
\(\text{Từ (1) và (2)}\Rightarrow MN\text{// và =}\frac{1}{2}BC\left(đpcm\right)\)