-3x2+6x+4
tìm giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 4 2019
Chọn C.
Áp dụng kết quả cơ bản
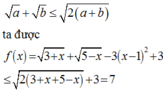
Đẳng thức xảy ra khi và chỉ khi x = 1
30 tháng 8 2021
a) \(A=x^2-4x+1=\left(x-2\right)^2-3\ge-3\)
\(minA=-3\Leftrightarrow x=2\)
b) \(B=-x^2-8x+5=-\left(x+4\right)^2+21\le21\)
\(maxB=21\Leftrightarrow x=-4\)
c) \(C=2x^2-8x+19=2\left(x-2\right)^2+11\ge11\)
\(minC=11\Leftrightarrow x=2\)
d) \(D=-3x^2-6x+1=-3\left(x+1\right)^2+4\le4\)
\(maxD=4\Leftrightarrow x=-1\)
HQ
2
6 tháng 9 2023
a: =4(x^2-3/2x-5)
=4(x^2-2*x*3/4+9/16-89/16)
=4(x-3/4)^2-89/4>=-89/4
Dấu = xảy ra khi x=3/4
b: =3(x^2-8/3x+1)
=3(x^2-2*x*4/3+16/9-7/9)
=3(x-4/3)^2-7/3>=-7/3
Dấu = xảy ra khi x=4/3
AH
Akai Haruma
Giáo viên
6 tháng 9 2023
Lời giải:
a. $A=4x^2-6x-20=(2x)^2-2.2x.\frac{3}{2}+(\frac{3}{2})^2-\frac{89}{4}$
$=(2x-\frac{3}{2})^2-\frac{89}{4}$
Vì $(2x-\frac{3}{2})^2\geq 0$ với mọi $x$
$\Rightarrow A\geq 0-\frac{89}{4}=\frac{-89}{4}$
Vậy $A_{\min}=\frac{-89}{4}$. Giá trị này đạt tại $2x-\frac{3}{2}=0$
$\Leftrightarrow x=\frac{3}{4}$
b.
$B=3x^2-8x+1=3(x^2-\frac{8}{3}x)+1$
$=3[x^2-2.x.\frac{4}{3}+(\frac{4}{3})^2]-\frac{13}{3}$
$=3(x-\frac{4}{3})^2-\frac{13}{3}\geq 3.0-\frac{13}{3}=\frac{-13}{3}$
Vậy $B_{\min}=\frac{-13}{3}$. Giá trị này đạt tại $x-\frac{4}{3}=0$
$\Leftrightarrow x=\frac{4}{3}$
KC
1
16 tháng 10 2021
\(A=3x^2+6x+15=3\left(x^2+2x+1\right)+12\)
\(=3\left(x+1\right)^2+12\ge12\)
\(minA=12\Leftrightarrow x=-1\)
PT
1
5 tháng 9 2021
\(\left(n^2+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\ge\dfrac{1}{4}-\dfrac{3}{4}=-\dfrac{1}{2}\forall n\)
Dấu '=' xảy ra khi n=0
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
CM
30 tháng 1 2017
Đáp án D
f x = 2 x 3 - 3 x 2 - 12 x + 10 ⇔ f ' x = 6 x 2 - 6 x - 12 ⇔ x = - 1 ; x = 2
So sánh f - 3 = - 35 , f - 1 = 17 , f 2 = - 10 , f 3 = 1
m a x [ - 3 ; 3 ] f x = 17 ; m i n [ - 3 ; 3 ] f x = - 35 .
