(x +1/2)-2/3= cân bậc 16/9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
3
27 tháng 12 2022
`sqrt 16 = 4`.
`sqrt(4^2) = 4`.`
`-sqrt 81 = -9`.
DQ
2
28 tháng 3 2020
- Ta có: \(A=\frac{\sqrt{x+1}}{\sqrt{x-1}}\)
- Thay \(x=\frac{16}{9}\)vào đa thức \(A,\)ta có:
\(A=\frac{\sqrt{\frac{16}{9}+1}}{\sqrt{\frac{16}{9}-1}}\)
\(\Leftrightarrow A=\frac{\sqrt{\frac{25}{9}}}{\sqrt{\frac{7}{9}}}\)
\(\Leftrightarrow A=\frac{5\sqrt{7}}{7}\)
Vậy \(A=\frac{5\sqrt{7}}{7}\)
28 tháng 3 2020
Thay x = 16/9 vào biểu thức, ta có:
\(\frac{\sqrt{\frac{16}{9}+1}}{\sqrt{\frac{16}{9}-1}}=\frac{\sqrt{\frac{25}{9}}}{\sqrt{\frac{7}{9}}}=\frac{\frac{5}{3}}{\frac{\sqrt{7}}{3}}=\frac{5\sqrt{7}}{5}\)
9 tháng 6 2018
a) ( x - 3)4 + ( x - 5)4 = 82
Đặt : x - 4 = a , ta có :
( a + 1)4 + ( a - 1)4 = 82
⇔ a4 + 4a3 + 6a2 + 4a + 1 + a4 - 4a3 + 6a2 - 4a + 1 = 82
⇔ 2a4 + 12a2 - 80 = 0
⇔ 2( a4 + 6a2 - 40) = 0
⇔ a4 - 4a2 + 10a2 - 40 = 0
⇔ a2( a2 - 4) + 10( a2 - 4) = 0
⇔ ( a2 - 4)( a2 + 10) = 0
Do : a2 + 10 > 0
⇒ a2 - 4 = 0
⇔ a = + - 2
+) Với : a = 2 , ta có :
x - 4 = 2
⇔ x = 6
+) Với : a = -2 , ta có :
x - 4 = -2
⇔ x = 2
KL.....
b) ( n - 6)( n - 5)( n - 4)( n - 3) = 5.6.7.8
⇔ ( n - 6)( n - 3)( n - 5)( n - 4) = 1680
⇔ ( n2 - 9n + 18)( n2 - 9n + 20) = 1680
Đặt : n2 - 9n + 19 = t , ta có :
( t - 1)( t + 1) = 1680
⇔ t2 - 1 = 1680
⇔ t2 - 412 = 0
⇔ ( t - 41)( t + 41) = 0
⇔ t = 41 hoặc t = - 41
+) Với : t = 41 , ta có :
n2 - 9n + 19 = 41
⇔ n2 - 9n - 22 = 0
⇔ n2 + 2n - 11n - 22 = 0
⇔ n( n + 2) - 11( n + 2) = 0
⇔ ( n + 2)( n - 11) = 0
⇔ n = - 2 hoặc n = 11
+) Với : t = -41 ( giải tương tự )
TT
8 tháng 6 2018
@Giáo Viên Hoc24.vn
@Giáo Viên Hoc24h
@Giáo Viên
@giáo viên chuyên
@Akai Haruma
23 tháng 9 2023
Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:
b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:
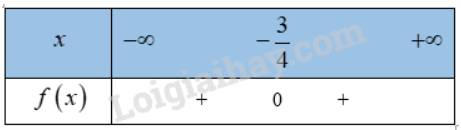
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
1 tháng 3 2020
a)(Sửa đề) \(4(x^2-6x+9)-16(4x^2+28x+49)=0\)
\(⇔(2x-6)^2-(8x+28)^2=0\)
\(⇔(-6x-34)(10x+22)=0\)
\(⇔\left[\begin{array}{} -6x-34=0\\ 10x+22=0 \end{array}\right.\)
\(⇔\left[\begin{array}{} x=-\dfrac{17}{3}\\ x=-\dfrac{11}{5} \end{array}\right.\)
b)(Sửa đề 1) \((2x-16)^2-(x-4)^2=0\)
\(⇔(3x-20)(x-12)=0\)
\(⇔\left[\begin{array}{} 3x-20=0\\ x-12=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=\frac{20}{3}\\ x=12 \end{array}\right.\)
(Sửa đề 2) \((x^2-16)^2-(x-4)^2=0\)
\(⇔(x^2-x-12)(x^2+x-20)=0\)
\(⇔(x-4)^2(x+3)(x+5)=0\)
\(⇔\left[\begin{array}{} (x-4)^2=0\\\ x+3=0\\ x+5=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=4\\\ x=-3\\ x=-5 \end{array}\right.\)
\(\left(x+\frac{1}{2}\right)-\frac{2}{3}=\sqrt{\frac{16}{9}}\)
=> \(\left(x+\frac{1}{2}\right)-\frac{2}{3}=\frac{4}{3}\)
=> \(x+\frac{1}{2}=\frac{4}{3}+\frac{2}{3}=\frac{6}{3}=2\)
=> \(x=2-\frac{1}{2}=\frac{3}{2}\)