Cho tam giác ABC có Aˆ=90o,Bˆ=60o. Kẻ AH vuông góc với BC (H ∈ BC)
So sánh HACˆ và ABCˆ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔABC có
BA<BC(gt)
mà góc đối diện với cạnh BA là \(\widehat{ACB}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABH vuông tại H và ΔAMH vuông tại H có
HB=HM(gt)
AH chung
Do đó: ΔABH=ΔAMH(hai cạnh góc vuông)
Suy ra: BA=MA(hai cạnh tương ứng)
Xét ΔBAM có BA=MA(cmt)
nên ΔBAM cân tại A(Định nghĩa tam giác cân)
Xét ΔBAM cân tại A có \(\widehat{B}=60^0\)(gt)
nên ΔBAM đều(Dấu hiệu nhận biết tam giác đều)

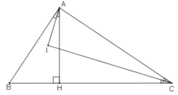
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.

a: Xét ΔADC có
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{ADH}=180^0-30^0-45^0\)
hay \(\widehat{ADH}=105^0\)

a) Xét ΔABC có Bˆ>CˆB^>C^
mà cạnh đối diện với góc B là AC
và cạnh đối diện với góc C là AB
nên AC>AB
hay AB<AC(Định lí 2 về quan hệ giữa cạnh và góc trong tam giác)
b) Xét ΔABC có AB<AC(cmt)
mà hình chiếu của AB trên BC là HB
và hình chiếu của AC trên BC là HC
nên HB<HC(định lí 2 về quan hệ giữa đường vuông góc, đường xiên và hình chiếu)
c) Xét ΔDBC có HB<HC(cmt)
mà hình chiếu của DB trên BC là HB
và hình chiếu của DC trên BC là HC
nên DB<DC(định lí 1 về quan hệ giữa đường vuông góc, đường xiên và hình chiếu)
Xét ΔDBC có DB<DC(cmt)
mà góc đối diện với DB là góc DCB
và góc đối diện với DC là góc DBC
nên DBCˆ>DCBˆDBC^>DCB^(định lí 1 về quan hệ giữa góc và cạnh trong tam giác)

Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
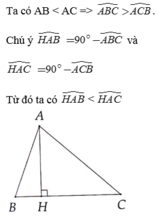

A B C H 60
Xét tam giác ABC vuông tại A
Ta có \(\widehat{BAC}=90^o\)(GT)
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=90^o\)( hai góc bù nhau )
Mà \(\widehat{ABC}=60^o\)(GT)
\(\Rightarrow\widehat{ACB}=30^o\)( Bù nhau )
Xét tam giác AHC vuông tại H ta có :
\(\widehat{ACH}=30^o\)(CMT)
\(\Rightarrow\widehat{ACH}+\widehat{HAC}=90^o\)( hai góc bù nhau )
\(\Rightarrow30^o+\widehat{HAC}=90^o\)
\(\Rightarrow\widehat{HAC}=60^o\)
Vì \(\widehat{ABC}=60^o\left(gt\right)\)
Có \(\widehat{HAC}=60^o\left(cmt\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{HAC}=60^o\)