với những giá trị Z nào của x thì giá trị của biểu thức sau :
9-2x phần x-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
29 tháng 1 2022
Lời giải:
Để $P=\frac{9-2x}{x-3}$ nguyên thì:
$9-2x\vdots x-3$
$\Leftrightarrow 3-2(x-3)\vdots x-3$
$\Leftrightarrow 3\vdots x-3$
Khi đo $x-3$ là ước của $3$
$\Leftrightarrow x-3\in\left\{\pm 1; \pm 3\right\}$
$\Leftrightarrow x\in \left\{4; 2; 6; 0\right\}$
PT
1
CM
11 tháng 10 2019
Ta có: 3 x 2 + 2x -1 = 2 3 x + 3 ⇔ 3 x 2 + 2x - 2 3 x -3 -1 = 0
⇔ 3 x 2 + (2 - 2 3 )x -4 =0 ⇔ 3 x 2 + 2(1 - 3 )x -4 = 0
∆ ' = b ' 2 – ac= 1 - 3 2 - 3 (-4) =1 - 2 3 +3 +4 3
= 1 + 2 3 +3 = 1 - 3 2 > 0
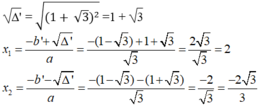
Vậy với x= 2 hoặc x = (-2 3 )/3 thì giá trị của hai biểu thức trên bằng nhau
CM
12 tháng 8 2018
Ta có: x 2 - 2 3 x - 3 = 2 x 2 +2x + 3
⇔ x 2 - 2 3 x - 3 - 2 x 2 -2x - 3 =0
⇔ x 2 +2x +2 3 x +2 3 =0
⇔ x 2 + 2(1 + 3 )x + 2 3 =0
∆ ' = b ' 2 – ac= 1 + 3 2 – 1. 2 3 = 1 + 2 3 + 3 -2 3 = 4 > 0
∆ ' = 4 =2
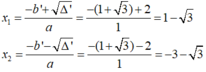
Vậy với x=1 - 3 hoặc x = - 3 - 3 thì giá trị của hai biểu thức trên bằng nhau
PT
Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau? -2 2 x – 1 và 2 x 2 + 2x +3
1
CM
17 tháng 12 2017
Ta có: -2 2 x – 1 = 2 x 2 + 2x +3 ⇔ 2 x 2 +2x + 3 + 2 2 x + 1=0
⇔ 2 x 2 + 2(1 + 2 )x +4 =0
∆ ' = b ' 2 – ac= 1 + 2 2 - √2 .4= 1+2 2 +2 - 4 2
= 1-2 2 +2 = 2 - 1 2 > 0
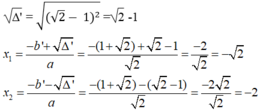
Vậy với x= - 2 hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau
CM
9 tháng 3 2018
Từ giả thiết suy ra (x + 1)2 - 4 ≤ (x - 3)2
Û x2 + 2x + 1 - 4 ≤ x2 - 6x + 9
Û x2 + 2x + 1 - 4 - x2 + 6x - 9 ≤ 0
Û 8x ≤ 12
Û x ≤ 3/2
Vậy x ≤ 3/2là giá trị cần tìm.
Đáp án cần chọn là: C
TN
11 tháng 1 2017
bài này ko hay cho lắm, cách làm cụ thể nhất trong cái nhất r` đấy
a)Ta thấy: \(\left|x-5\right|\ge0\)
\(\Rightarrow-\left|x-5\right|\le0\)
\(\Rightarrow1000-\left|x-5\right|\le1000\)
\(\Rightarrow A\le1000\)
Dấu "=" xảy ra khi \(\left|x-5\right|=0\Leftrightarrow x=5\)
Vậy \(Max_A=1000\) khi \(x=5\)
b)Ta thấy: \(\left|y-3\right|\ge0\)
\(\Rightarrow\left|y-3\right|+50\ge50\)
\(\Rightarrow B\ge50\)
Dấu "="xảy ra khi \(\left|y-3\right|=0\Leftrightarrow y=3\)
Vậy \(Min_B=50\) khi \(y=3\)
c)Ta thấy: \(\hept{\begin{cases}\left|x-100\right|\ge0\\\left|y+200\right|\ge0\end{cases}}\)
\(\Rightarrow\left|x-100\right|+\left|y+200\right|\ge0\)
\(\Rightarrow\left|x-100\right|+\left|y+200\right|-1\ge-1\)
\(\Rightarrow C\ge-1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left|x-100\right|=0\\\left|y+200\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x=100\\y=-200\end{cases}}\)
Vậy \(Min_C=-1\) khi \(\hept{\begin{cases}x=100\\y=-200\end{cases}}\)
sssssssssssssssss
bạn nào trả lơif giup mình đi mình đang cần gấp lắm