Bài 1. Tính số đo xx và yy ở các hình 47.48.49,50,51:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Vì MN//BC nên \(\widehat {AMN} = \widehat {ABC}\)( 2 góc đồng vị), mà \(\widehat {ABC} = 60^\circ \)nên \(\widehat {AMN} = 60^\circ \)
Vì \(\widehat {AMN} + \widehat {BMN} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {BMN} = 180^\circ \\ \Rightarrow \widehat {BMN} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vì \(\widehat {ANM} + \widehat {MNC} = 180^\circ \)(2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ANM} + 150^\circ = 180^\circ \\ \Rightarrow \widehat {ANM} = 180^\circ - 150^\circ = 30^\circ \end{array}\)
Vì MN//BC nên \(\widehat {ANM} = \widehat {ACB}\) ( 2 góc đồng vị), mà \(\widehat {ANM} = 30^\circ \)nên \(\widehat {ACB} = 30^\circ \).
2. Vì xx’//yy’ nên \(\widehat {x'AB} = \widehat {ABy}\)( 2 góc so le trong)
Mà zz’\( \bot \) xx’ nên \(\widehat {x'AB} = 90^\circ \)
Do đó, \(\widehat {ABy} = 90^\circ \) nên zz’ vuông góc với yy’.

Ta có :
`@)` `\hat{x'Oy'} = \hat{xOy} = 100^@` (hai góc đối đỉnh)
`@)` `\hat{xOy + \hat{xOy'} = 180^@`
hay `100 +` `\hat{xOy'} = 180^@`
`⇒\hat{xOy'} = 180^@ - 100^@ = 80^@`
`@)` `\hat{x'Oy} = \hat{xOy'} = 80^@` (hai góc đối đỉnh)

x x' y y' A
Ta có :
xAy = 53 độ
+) Ta có :
xAy + yAx' = 180 độ (2 góc kề bù)
Mà xAy = 53 độ
=> 53 +độ + yAx' = 180 độ
=> yAx' = 180 độ - 53 độ
=> yAx' = 127 độ
+) Ta có :
xAy = x'Ay' (đối đỉnh)
Mà xAy = 53 độ
=> x'Ay' = 53 độ
+) Ta có :
yAx' = y'Ax (đối đỉnh)
Mà yAx' = 127 độ
=> y'Ax = 127 độ

x x' y y' O 45 độ
ta có: xx' cắt yy' tại O
=> góc xOy = góc x'Oy' =45 độ ( đối đỉnh)
=> góc x'Oy' = 45 độ
mà góc xOy + góc x'Oy = 180 độ ( kề bù)
Thay số: 45 độ + góc x'Oy = 180 độ
góc x'Oy = 180 độ - 45 độ
góc x'Oy = 135 độ
mà góc x'Oy = góc xOy' = 135 độ ( đối đỉnh)
=> góc xOy' = 135 độ

Vẽ hai đường thẳng xx" và yy" theo đề bài: góc xOy=x"Oy" =100 độ( Vì đây là hai góc đối đỉnh)
- góc xOy+xOy"=180 độ ( Vì đây là hai góc kề bù) => xOy"+100độ=180độ=> xOy"=180-100=80độ
Do xOy" và x"oy là hai góc đối đỉnh nên xOy"=x"Oy=80độ
Vì xOx" và yOy" là góc bẹt nên xOx"=yOy"=180độ
Vậy xOy=x"Oy"=100độ, xOy"=x"oy=80độ, xOx"=yOy"=180độ
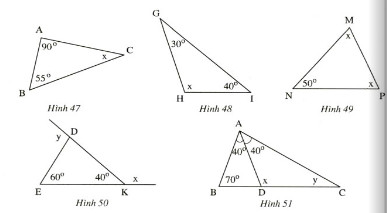
Tính số đo xx và yy ở các hình 47.48.49,50,51:
Giải:
Hình 47)
Theo dịnh lí tổng ba góc trong một tam giác ta được:
x+900+550=1800x+900+550=1800
⇒x=1800−(900+550)=350⇒x=1800−(900+550)=350
Hình 48)
Theo dịnh lí tổng ba góc trong một tam giác ta được:
x+400+300=1800x+400+300=1800
=>x=1800−(400+300)=1100=>x=1800−(400+300)=1100
Hình 49)
Theo dịnh lí tổng ba góc trong một tam giác ta được:
x+x+500=1800x+x+500=1800
⇒2x=1800−500=1300⇒2x=1800−500=1300
x=650x=650
Hình50)
Vì yy là góc ngoài tam giác nên ta có:
y=600+400=1000y=600+400=1000
Hai góc xx và ˆDKEDKE^ là hai góc kề bù nên:
x+400=1800x+400=1800
x=1800−400=1400x=1800−400=1400
Hình 51)
Áp dụng định lí tổng ba góc trong một tam giác vào ΔABCΔABC ta có:
ˆA+ˆB+ˆCA^+B^+C^
(400+400)+700+y=1800(400+400)+700+y=1800
y+1500=1800y+1500=1800
y=1800−1500=300y=1800−1500=300
Áp dụng định lí tổng ba góc trong một tam giác vào ΔACDΔACD ta có:
x+400+300=1800x+400+300=1800
x=1800−(400+300)=1100