<33 , giải phương trình và bất phương trình sau :
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
KM
1
NT
3
24 tháng 2 2018
x + 1/x < 2
<=> x^2/x + 1/x < 2x/x
<=> x^2+1/x < 2x/x
<=> x^2+1/x - 2x/x < 0
<=> x^2+1-2x/x < 0
<=> x^2-2x+1/x < 0
<=> (x-1)^2/x < 0
Vì (x-1)^2 >= 0
mà (x-1)^2/x < 0 => (x-1)^2 > 0 ; x < 0 <=> x < 0
Vậy x < 0
Tk mk nha
24 tháng 2 2018
\(\frac{x+1}{x}< 2\) \(ĐKXĐ:x\ne0\)
\(\frac{x+1}{x}-2< 0\)
\(\frac{x+1}{x}-\frac{2x}{x}< 0\)
\(\frac{x+1-2x}{x}< 0\)
\(\frac{1-x}{x}< 0\)
\(\Leftrightarrow\hept{\begin{cases}1-x>0\\x< 0\end{cases}}\) hoặc \(\hept{\begin{cases}1-x< 0\\x>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1\\x< 0\end{cases}}\) ( vô lí ) hoặc \(\hept{\begin{cases}x< 1\\x>0\end{cases}}\)
hay \(0< x< 1\)
H
11 tháng 5 2023
`|5x| = - 3x + 2`
Nếu `5x>=0<=> x>=0` thì phương trình trên trở thành :
`5x =-3x+2`
`<=> 5x +3x=2`
`<=> 8x=2`
`<=> x= 2/8=1/4` ( thỏa mãn )
Nếu `5x<0<=>x<0` thì phương trình trên trở thành :
`-5x = -3x+2`
`<=>-5x+3x=2`
`<=> 2x=2`
`<=>x=1` ( không thỏa mãn )
Vậy pt đã cho có nghiệm `x=1/4`
__
`6x-2<5x+3`
`<=> 6x-5x<3+2`
`<=>x<5`
Vậy bpt đã cho có tập nghiệm `x<5`
VD
0
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
PT
1
PT
1
PT
1
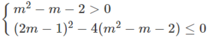
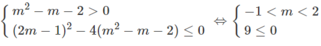
a, \(\left(2x-1\right)^2-x\left(x-3\right)=1\Leftrightarrow4x^2-4x+1-x^2+3x=1\)
\(\Leftrightarrow3x^2-x=0\Leftrightarrow x\left(3x-1\right)=0\Leftrightarrow x=0;x=\frac{1}{3}\)
Vậy tập nghiệm phương trình là S = { 0 ; 1/3 }
b, \(\frac{1}{x+2}+\frac{3}{3-x}=\frac{5x}{x^2-x-6}\)ĐK : \(x\ne-2;3\)
\(\Leftrightarrow\frac{x-3-3\left(x+2\right)}{\left(x-3\right)\left(x+2\right)}=\frac{5x}{\left(x-3\right)\left(x+2\right)}\Rightarrow-2x-9=5x\)
\(\Leftrightarrow-7x=9\Leftrightarrow x=-\frac{9}{7}\)( tm )
Vậy tập nghiệm của phương trình là S = { -9/7 }
c, \(\frac{x+3}{5}-\frac{3-x}{3}>\frac{2x-3}{2}\)
\(\Leftrightarrow\frac{3x+9-15+5x}{15}-\frac{2x-3}{2}>0\)
\(\Leftrightarrow\frac{8x-6}{15}-\frac{2x-3}{2}>0\Leftrightarrow\frac{16x-12-30x+45}{30}>0\)
\(\Rightarrow-14x+33>0\)vì 30 > 0
\(\Leftrightarrow x< \frac{33}{14}\)Vậy tập nghiệm BFT là S = { x | x < 33/14 }