Số tự nhiên x thỏa mãn 2.3x+3x+2=99
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
VD
2

NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 10 2023
3\(x\) + 54: 2 = 99
3\(x\) + 27 = 99
3\(x\) = 99 - 27
3\(x\) = 72
\(x\) = 72: 3
\(x\) = 24

6 tháng 9 2015
2.3x + 3x+2 = 99.312
3x.(2+32) = 9.11.312
3x.11 = 11.312.32
3x = 314
x=14
NH
2

15 tháng 12 2015
2.3x +32.3x = 99
3x ( 2 +9) = 99
3x .11 = 99
3x =9 =32
x =2
TT
3

15 tháng 11 2015
9x+17 = = 3(3x+2) +11 chia hết cho 3x+2
=> 11 chia hết cho 3x+2
=> x là số N
=> 3x+2 =11 => 3x =9
=> x =3
HT
15 tháng 11 2015
9x + 17 chia hết cho 3x + 2
=> 9x + 6 + 11 chia hết cho 3x + 2
Vì 9x + 6 chia hết cho 3x + 2
=> 11 chia hết cho 3x + 2
=> 3x + 2 thuộc Ư(11)
| 3x+2 | x |
| 1 | KTM |
| 11 | 3 |
KL: x = 3
HN
0

TB
1

11 tháng 11 2015
9x+17 = 3(3x+2) +11 chia hết cho 3x+2 khi 11 chia hết cho 3x+2
Vậy 3x+2 là Ư(11) ={ 1;11}
3x+2 = 1 => loại
3x+2 = 11 => 3x =9 => x =3
Vậy x =3
NT
2

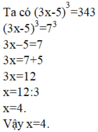
x\(\in\) ∅