Tính tích S tất cả các nghiệm nguyên khác 0 của phương trình |x-2|+|x+3|=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
13 tháng 3 2020
+) Xét khoảng \(x< -3\)
Khi đó \(pt\Leftrightarrow\left(3-x\right)+\left(-x-3\right)=6\)
\(\Leftrightarrow-2x=6\Leftrightarrow x=-3\)(gt này không thuộc khoảng đang xét)
+) Xét khoảng \(-3\le x\le3\)
Khi đó \(pt\Leftrightarrow\left(3-x\right)+\left(x+3\right)=6\)
\(\Leftrightarrow6=6\)(luôn đúng với \(-3\le x\le3\))
+) Xét khoảng x > 3
Khi đó \(pt\Leftrightarrow\left(x-3\right)+\left(x+3\right)=6\)
\(\Leftrightarrow2x=6\Leftrightarrow x=3\)(gt này không thuộc khoảng đang xét)
Từ đó suy ra nghiệm của phương trình |x-3|+|x+3|=6 trong khoảng từ \(-3\rightarrow3\)
Các nghiệm nguyên dương là: 1;2;3
Suy ra tích S = 1.2.3 = 6
Vậy S = 6
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 11 2023
\(x^5\) - 2\(x^4\) - (y2 + 3)\(x\) + 2y2 - 2 = 0
(\(x^5\) - 2\(x^4\))- (y2 + 3)\(x\) + 2.(y2 + 3) - 8 = 0
\(x^4\).(\(x\) - 2) - (y2 + 3).(\(x\) - 2) - 8 = 0
(\(x\) - 2).(\(x^4\) - y2 - 3) = 8
8 = 23; Ư(8) = {-8; - 4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
| \(x-2\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(x\) | -6 | -2 | 0 | 1 | 3 | 4 | 6 | 10 |
| \(x^4\) - y2 - 3 | -1 | -2 | -4 | -8 | 8 | 4 | 2 | 1 |
| y | \(\pm\)\(\sqrt{1294}\) | \(\pm\)\(15\) | \(\pm\)1 | \(\pm\)\(\sqrt{6}\) | y2 = -10 (ktm) | \(\pm\)\(\sqrt{249}\) | \(\pm\)\(\sqrt{1291}\) | \(\pm\)\(\sqrt{9996}\) |
vì \(x\); y nguyên nên theo bảng trên ta có các cặp \(x\); y thỏa mãn đề bài là:
(\(x\); y) = (0; -1;); (0; 1)
CM
28 tháng 6 2019
Chọn D.
Đặt t = 2x + 2-x, suy ra t2 = 22x + 2 -2x + 2.
Ta có 
Phương trình trở thành
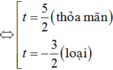
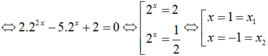
khi đó ; S = x1+ x2 = 0.
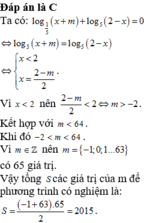
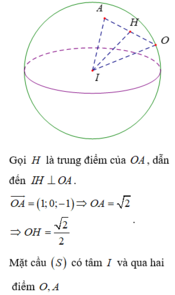
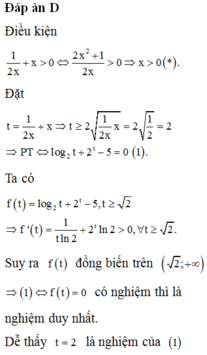
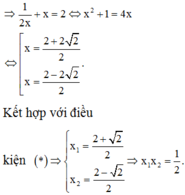
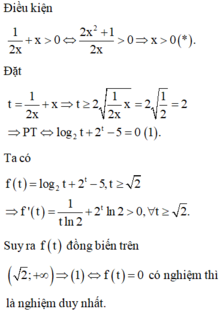
lập bảng xét dấu
x -3 2
x-2 - | - 0 +
x+3 - 0 + | +
Xét khoảng x<=3
=> |x-2|+|x+3|=5 <=> -x+2-x-3=5
<=> -3 (TM)
Xét khoảng -3<x<=2
=> |x-2|+|x+3|=5 <=> -x+2+x+3=5
<=> 0x=0 <=> x=-2;-1;0;1;2
Xét khoảng x>2
=> |x-2|+|x+3|=5 <=> x-2+x+3 =5
<=> x=0 (ko thỏa mãn)
Vậy X= -3;-2;-1;0;1;2