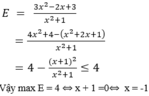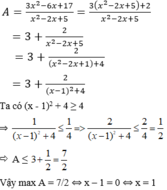Tìm giá trị nhỏ nhất của A = 3x2-2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 9 2017
ĐKXĐ của phân thức x ≠ 1.
Ta có:
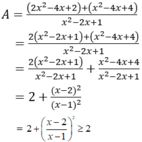
Vậy min A = 2 khi và chỉ khi x - 2 = 0 ⇔ x =2
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
TL
1
23 tháng 10 2021
\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)
MT
1
29 tháng 8 2021
1: Ta có: \(x^2-2x-5\)
\(=x^2-2x+1-6\)
\(=\left(x-1\right)^2-6\ge-6\forall x\)
Dấu '=' xảy ra khi x=1
2: ta có: \(3x^2+5x-2\)
\(=3\left(x^2+\dfrac{5}{3}x-\dfrac{2}{3}\right)\)
\(=3\left(x^2+2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}-\dfrac{49}{36}\right)\)
\(=3\left(x+\dfrac{5}{6}\right)^2-\dfrac{49}{12}\ge-\dfrac{49}{12}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{5}{6}\)
PT
1
13 tháng 11 2021
\(A=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow x=1\\ B=2\left(x^2-3x\right)=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{9}{2}\\ B=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\\ B_{min}=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\\ C=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\\ C_{max}=7\Leftrightarrow x=2\)
13 tháng 11 2021
a,\(A=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu "=" \(\Leftrightarrow x=-1\)
b,\(B=2\left(x^2-3x\right)=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu "=" \(\Leftrightarrow x=\dfrac{3}{2}\)
c,\(=C=-\left(x^2-4x-3\right)=-\left[\left(x^2-4x+4\right)-7\right]=-\left(x-2\right)^2+7\le7\)
Dấu "=" \(\Leftrightarrow x=2\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 12 2021
\(A=2\left(x^2-2xy+y^2\right)+\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{8067}{4}\)
\(A=2\left(x-y\right)^2+\left(x-\dfrac{3}{4}\right)^2+\dfrac{8067}{4}\ge\dfrac{8067}{4}\)
\(A_{min}=\dfrac{8067}{4}\) khi \(x=y=\dfrac{3}{2}\)
HQ
2
6 tháng 9 2023
a: =4(x^2-3/2x-5)
=4(x^2-2*x*3/4+9/16-89/16)
=4(x-3/4)^2-89/4>=-89/4
Dấu = xảy ra khi x=3/4
b: =3(x^2-8/3x+1)
=3(x^2-2*x*4/3+16/9-7/9)
=3(x-4/3)^2-7/3>=-7/3
Dấu = xảy ra khi x=4/3
AH
Akai Haruma
Giáo viên
6 tháng 9 2023
Lời giải:
a. $A=4x^2-6x-20=(2x)^2-2.2x.\frac{3}{2}+(\frac{3}{2})^2-\frac{89}{4}$
$=(2x-\frac{3}{2})^2-\frac{89}{4}$
Vì $(2x-\frac{3}{2})^2\geq 0$ với mọi $x$
$\Rightarrow A\geq 0-\frac{89}{4}=\frac{-89}{4}$
Vậy $A_{\min}=\frac{-89}{4}$. Giá trị này đạt tại $2x-\frac{3}{2}=0$
$\Leftrightarrow x=\frac{3}{4}$
b.
$B=3x^2-8x+1=3(x^2-\frac{8}{3}x)+1$
$=3[x^2-2.x.\frac{4}{3}+(\frac{4}{3})^2]-\frac{13}{3}$
$=3(x-\frac{4}{3})^2-\frac{13}{3}\geq 3.0-\frac{13}{3}=\frac{-13}{3}$
Vậy $B_{\min}=\frac{-13}{3}$. Giá trị này đạt tại $x-\frac{4}{3}=0$
$\Leftrightarrow x=\frac{4}{3}$
CM
30 tháng 4 2018
Đáp án D.
Sử dụng máy tính cầm tay chức năng TABLE với thiết lập Start ‒5; End 5; Step 1 thì ta có
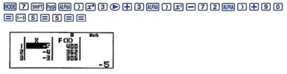
Từ bảng giá trị ta kết luận được giá trị lớn nhất của hàm số đạt được là 400 khi x = − 5 .
Từ bảng giá trị trên ta chưa thể kết luận được giá trị nhỏ nhất của hàm số.
Ta thấy x 3 + 3 x 2 − 72 x + 90 ≥ 0, ∀ x ∈ ℝ .
Dấu bằng xảy ra khi x 3 + 3 x 2 − 72 x + 90 = 0 .
Trong ba nghiệm trên ta thấy nghiệm x 3 ∈ − 5 ; 5 . Từ đây ta có thể kết luận giá trị nhỏ nhất của hàm số đạt được là 0 khi x = x 3 .
Vậy tổng cần tìm là 400. Ta chọn D.