Vẽ hai góc kề bù ∠xOy và yOx' , biết ∠xOy = 70o. Gọi Ot là tia phân giác của xOy , Ot' là tia phân giác x'Oy . Tính ∠yOx' , ∠tOt' , ∠xOt'.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tự vẽ hình nha ==''
xOy + yOx' = 1800 (2 góc kề bù)
1200 + yOx' = 1800
yOx' = 1800 - 1200
yOx' = 600
Ot là tia phân giác của xOy
=> xOt = tOy = xOy : 2 = 120 : 2 = 600

Ta có yOx' = 180o-110o=70o
Ot là phân giác của xOy =>tOy=xOt=1/2xOy=110o:2=55o
Mà x'Ot=x'Oy+tOy
=>x'Ot=55o+70o=125o
y t x x'
Vì Ot là tia phân giác\(\widehat{xOy}\) của nên \(\widehat{xOt}\)=\(\widehat{yOt}\)=\(\frac{\widehat{xOy}}{2}\)= 55
Vì \(\widehat{xOy}\)và \(\widehat{yOx'}\)là hai góc kề bù nên \(\widehat{xOy}\)+\(\widehat{yOx'}\)=180
110 + \(\widehat{yOx'}\)=180
\(\widehat{yOx'}\)=70
Ta có: \(\widehat{yOx'}\)+ \(\widehat{yOt}\)= \(\widehat{x'Ot}\)
70 + 55 =\(\widehat{x'Ot}\)
\(\widehat{x'Ot}\)= 125

\(xOy+yOx'=180^0\) (2 góc kề bù)
\(110^0+yOx'=180^0\)
\(yOx'=180^0-110^0\)
\(yOx'=70^0\)
Om là tia phân giác của xOy
=> \(xOm=mOy=\frac{xOy}{2}=\frac{110^0}{2}=55^0\)
On là tia phân giác của yOx'
=> \(x'On=nOy=\frac{x'Oy}{2}=\frac{70^0}{2}=35^0\)
\(mOn=nOy+yOm\)
\(mOn=35^0+55^0\)
\(mOn=90^0\)
Chúc bạn học tốt![]()

Trả lời:
góc x'Om= 55+70 =125 độ
góc xOn= 110+35 =145 độ
góc nOm= 35+55= 90 độ
O x y x' m n
Vì 2 góc xoy và yox' là hay góc kề bù
=> Tia Oy nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{xOy}+\widehat{yOx'}=\widehat{xOx'}\)
hay \(110^0+\widehat{yOx'}=180^0\)
\(\Rightarrow\widehat{yOx'}=70^0\)
Vì tia Om là tia phân giác của góc xOy ta có :
\(\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=\frac{110^0}{2}=55^0\)
Vì tia On là tia phân giác của góc yOx' ta có :
\(\widehat{yOn}=\widehat{nOx'}=\frac{\widehat{yOx'}}{2}=\frac{70^0}{2}=35^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta có : \(\widehat{xOm}< \widehat{xOx'}\left(55^0< 180^0\right)\)
=> Tia Om nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{xOm}+\widehat{x'Om}=\widehat{xOx'}\)
hay \(55^0+\widehat{x'Om}=180^0\)
\(\Rightarrow\widehat{x'Om}=125^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta có : \(\widehat{nOx'}< \widehat{xOx'}\left(35^0< 180^0\right)\)
=> Tia On nằm giữa 2 tia Ox và Ox'
Ta có :
\(\widehat{nOx}+\widehat{nOx'}=\widehat{xOx'}\)
hay \(\widehat{nOx}+35^0=180^0\)
\(\Rightarrow\widehat{nOx}=145^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia xx'
Ta thấy Tia Oy nằm giữa 2 tia Ox và Ox'
hay tia Oy cũng nằm giữa 2 tia Om và On
Ta có :
\(\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
hay \(55^0+35^0=\widehat{mOn}\)
\(\Rightarrow\widehat{mOn}=90^0\)
Vậy \(\widehat{x'Om}=125^0;\)\(\widehat{xOn}=145^0\)và \(\widehat{nOm}=90^0\)

Ta có
xOy + x'Oy = 180o (Kề bù)
mà xOy = 80o
=> x'Oy = 100o
Vì Oz là phân giác của x'Oy
=> x'Oz = zOy = \(\frac{1}{2}x'Oy\)= 50o
Số đo góc xOz là
80 + 50 = 130 độ
K cho mk nha

1) Ta có: xOy^ = 3* yOx'^
và xOy^ + yOx'^ = 180o
=> 3* yOx'^ + yOx'^ = 180o
4* yOx'^ = 180o
yOx'^ = 45o
=> xOy^ = 3* yOx'^ = 3* 45o = 135o
Vậy yOx'^ = 45o
xOy^ = 135o
2) Ta có: xOy^ + yOx' = 180o (kề bù)
yOm^ = xOy^ /2
yOn^ = yOx'/2
và \(mOn=yOm+yOn\)
\(\Rightarrow mOn=\frac{xOy}{2}+\frac{yOx'}{2}\)
\(=\frac{xOy+yOx'}{2}\)
\(=\frac{180o}{2}\)
\(=90o\)
Vậy mOn^ = 90o

O x z y
Giải : Ta có : \(\widehat{xOy}+\widehat{yOz}=180^0\)(kề bù)
=> góc yOz = 1800 - góc xOy
=> góc yOz = 1800 - 1300
=> góc yOz = 500
Vậy ...
x O x' y 130 o ?
Vì 2 góc xOy và yOx' là 2 góc kề bù nên :
\(\widehat{xOy}+\widehat{yOx'}=180^0\)
\(130^0+\widehat{yOx'}=180^0\)
\(\widehat{yOx'}=180^0-130^0=50^0\).
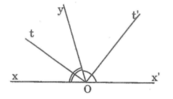
Giải:
O x x' t y t'
Vì \(x\widehat{O}y\) và \(y\widehat{O}x'\) là 2 góc kề bù
\(\Rightarrow x\widehat{O}y+y\widehat{O}x'=180^o\)
\(70^o+y\widehat{O}x'=180^o\)
\(y\widehat{O}x'=180^o-70^o\)
\(y\widehat{O}x'=110^o\)
Vì Ot là tia p/g của \(x\widehat{O}y\)
\(\Rightarrow x\widehat{O}t=t\widehat{O}y=\dfrac{x\widehat{O}y}{2}=\dfrac{70^o}{2}=35^o\)
Vì Ot' là tia p/g của \(y\widehat{O}x'\)
\(\Rightarrow y\widehat{O}t'=t'\widehat{O}x'=\dfrac{y\widehat{O}x'}{2}=\dfrac{110^o}{2}=55^o\)
\(\Rightarrow t\widehat{O}y+y\widehat{O}t'=t\widehat{O}t'\)
\(35^o+55^o=t\widehat{O}t'\)
\(\Rightarrow t\widehat{O}t'=90^o\)
\(\Rightarrow x\widehat{O}y+y\widehat{O}t'=x\widehat{O}t'\)
\(70^o+55^o=x\widehat{O}t'\)
\(\Rightarrow x\widehat{O}t'=125^o\)
Chúc bạn học tốt!