A B M C Chứng minh tam giác BAM= tam giác CAM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2023
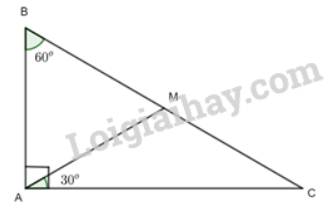
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.
QK
30 tháng 12 2020
A B C M a) Xét tam giác BAM và tam giác CAM có : BA = CA (GT) Góc BAM=góc CAM ( vì : AM là tia phân giác của góc BAC ) AM là cạnh chung Do đó: tam giác BAM = tam giác CAM(c.g.c) b) vì tam giác BAM = tam giác CAM (câu a) => góc AMB = góc AMC ( hai góc tương ứng) Mà : hai góc đó là hai góc kề bù Nên: Góc AMB=góc CAM = 90 độ => AM vuông góc với BC. D C) Xét tam giác BAD và tam giác CAD có: AB=AC( GT) BD=CD(GT) AD là cạnh chung =>Do đó :tam giác BAD=tam giác CAD(c.c.c) => AD là tia phân giác của góc A ( vì góc BAD=góc CAD) Nên: ba điểm A,D,M thẳng hàng => AM là đường trung trực của BC => AD cũng là đường trung trực của BC
20 tháng 2 2021
a) Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC(ΔABC cân tại A)
AM chung
Do đó: ΔAMB=ΔAMC(cạnh huyền-cạnh góc vuông)
Suy ra: MB=MC(hai cạnh tương ứng)
b) Ta có: ΔAMB=ΔAMC(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
c) Xét ΔDMB vuông tại D và ΔEMC vuông tại E có
MB=MC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDMB=ΔEMC(cạnh huyền-góc nhọn)
Suy ra: DM=EM(hai cạnh tương ứng)
Xét ΔMDE có MD=ME(cmt)
nên ΔMDE cân tại M(Định nghĩa tam giác cân)
NV
2
AD
4 tháng 2 2021
Tam giác ABC có :
BM=CM(GT)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
Một tam giác có tia phân giác đồng thời là đường trung tuyến thì là tam giác cân
=> Tam giác ABC cân tại A (đccm)
AD
4 tháng 2 2021
Ok cách khác
Kẻ \(MD\perp AB;ME\perp AC\)
Xét tam giác ADM và AEM, có :
\(\widehat{ADM}=\widehat{AEM}=90^o\)
\(\widehat{BAM}=\widehat{CAM}\left(gt\right)\)
AM-cạnh chung
=> Tam giác ADM=AEM(cạnh huyền-góc nhọn)
=> DM=ME
Xét tam giác BMD và CME,có :
DM=ME(cmt)
\(\widehat{MEC}=\widehat{MDB}=90^o\)
BM=CM(gt)
=> Tam giác BMD=CME(cạnh huyền-cạnh góc vuông)
=> \(\widehat{B}=\widehat{C}\)
=> Tam giác ABC cân tại A (2 góc đáy bằng nhau)
*Hơi dài dòng TÍ
28 tháng 11 2016
a). Ta có AM là đường trung trực của đoạn thẳng BC => AM\(\perp\) BC và BM=CM
Xét tam giác AMB vuông tại M và tam giác AMC vuông tại M có:
AM là cạnh chung.
BM=CM (cmt)
=> Tam giác AMB=tam giác AMC (hai cạnh góc vuông)
b). Tam giác AMB=tam giác AMC
=> AB=AC (hai cạnh tương ứng)
=> \(\widehat{BAM}\) = \(\widehat{CAM}\) (hai góc tương ứng)
=> \(\widehat{ABM}=\widehat{ACM}\) (hai góc tương ứng)
c). Xét tam giác ANB và tam giác ANC có:
AB=AC (cmt)
\(\widehat{BAN}=\widehat{CAN}\) (\(\widehat{BAM}=\widehat{CAM};N\in\) AM)
AN là cạnh chung.
=> Tam giác ANB=tam giác ANC (c.g.c)