Cho \(\Delta ABC\), \(\widehat{A}=2\widehat{B}\). Chứng minh: BC2 = AC2 + AB.AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


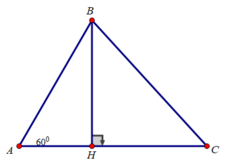
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
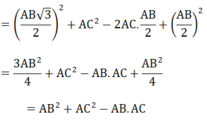
Vậy được điều phải chứng minh.

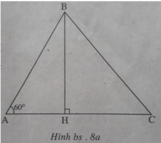
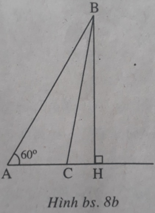
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C

Đầu tiên, vẽ tia p/g AD vì góc BAC =2ABC=>Có hai trường hợp sảy ra:1 ^ABD=^BAD=> Tam giác ADB cân tại D=>AD=BD(1)
2 ^ABC=^DAC=>tam giác ABC=tam giác DAC
[AB/AD=BC/AC=>AB.AC=BC.AD (theo(1))
[AC/BC=DC/AC<=>AC^2=BC/DC=BC(BC-BD)=BC^2-AB.AC
=>BC^2=AC^2+AB.AC

SỬA ĐỀ: "Chứng minh: \(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{MN.MP}{AB.AC}\)
Nếu bài này lớp 8 và đề như vậy theo mình không làm được vì:
Chưa học sin cos tan.....
Nếu c/m bằng tam giác đồng dạng thì thiếu dữ kiện

Mình sẽ làm từ câu C nha vì câu C có liên quan đến câu cuối
c/ Xét tam giác ABF và tam giác AEC ta có :
Góc BAF = góc CAE ( AF là phân giác)
góc ABF = góc AEC ( 2 góc nt chắn cung AC)
=>tam giác ABF đồng dạng tam giác AEC (g-g)
=>\(\frac{AB}{AE}=\frac{AF}{AC}\)=>AB.AC=AE.AF
d/ Xét tam giác ABF và tam giác CFE ta có:
góc ABF = góc FEC ( 2 góc nt chắn cung AC )
góc BAF = góc FCE (2 góc nt chắn cung EB )
=> tam giác ABF đồng dạng tam giác CEF (g-g)
=>\(\frac{FB}{FE}=\frac{FA}{FC}\)=>FB.FC=FA.FE
Ta có AF.AE=AB.AC (cmt)
AF.FE=BF.CF (cmt)
=> AF.AE-AF.FE = AB.AC - BF.CF
=> AF(AE-FE) = AB.AC - BF.CF
=> \(AF^2=AB.AC-BF.CF\)

a) Xét (O) có AE là tia phân giác của góc BAC
=> ^BAE=^CAE
=> sđBE=sđCE
=> BE=CE (liên hệ giữa cung và dây cung)
=> tam giác BEC cân tại E (đpcm)
b) Tứ giác ABEC nội tiếp (O)
=> ^BAC+^BEC=180 độ (2 góc đối nhau)
<=> ^BEC=180 độ - ^BAC
Tam giác ABC có ^BAC+^ABC+^BCA=180 độ
=> =180 độ - ^BAC=^ABC+^BCA
Suy ra Góc BEC = góc ABC + góc ACB (đpcm)
c) AE là tia phân giác của góc BAC
=> ^BAE=^CAE
Hay ^BAF=^CAE
Tứ giác ABEC nội tiếp (O)
=> ^ABC=^AEC (2 góc nt chắn cung AC)
Hay ^ABF=^AEC
Xét tam giác ABF và tam giác AEC có:
^ABF=^AEC
^BAF=^CAE
=> tam giác ABF ~ tam giác AEC (g-g)
=> AB/AF=AE/AC
<=> AB.AC=AE.AF (đpcm)

A B C M N P H K
Kẻ \(BH⊥AC;NK⊥MP\)
Khi đó ta thấy ngay \(\Delta MNK\sim\Delta ABH\left(g-g\right)\Rightarrow\frac{NK}{BH}=\frac{MN}{AB}\)
Lại có \(\frac{S_{MNP}}{S_{ABC}}=\frac{\frac{1}{2}.MP.NK}{\frac{1}{2}.AC.BH}=\frac{NK}{BH}.\frac{MP}{AC}=\frac{MN}{AB}.\frac{MP}{AC}=\frac{MN.MP}{AB.AC}\left(đpcm\right)\)

A, Có : góc HBA = góc ABC ( chung 1 góc )
=> tam giác HBA đông dạng với tam giác ABC ( g.g)
B, câu (A) => HA/AC = BA/BC
=> AB.AC = AH.BC
Tk mk nha