Với giá trị nào của a và b thì đa thức f(x)=x4-3x3+3x2+ax+bchia hết cho đa thức g(x)=x2+4-3x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2021
\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)
CM
18 tháng 12 2017
Ta có
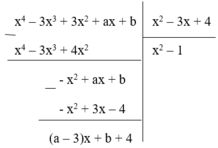
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
Đa thức f(x) là đa thức có bậc cao nhất là bậc 4 nên khi chia cho đa thức g(x) có bậc cao nhất là bậc 2 và không có dư thì được thương là đa thức bậc 2 . Suy ra
f(x) : g(x) = (x2 + cx + d)
<=> f(x) = g(x).(x^2 + cx + d)
<=> x4 - 3x3 + 3x2 + ax + b = (x2 - 3x + 4)(x2 + cx + d)
<=> x4 - 3x3 + 3x2 + ax + b = x4 + x3.(c - 3) + x2.(d - 3c + 4) + x(-3d + 4c) + 4d
Đồng nhất hai vế , ta sẽ tìm được a,b