Giải phương trình : x30 - x/45= 1/4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 3 2019
Ta có: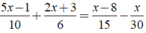
⇔ 15x - 3 + 10x + 15 = 2x - 16 - x
⇔ 25x - 2x + x = - 16 - 15 + 3
⇔ 24x = - 28 ⇔ x = - 7/6.
Vậy phương trình đã cho có tập nghiệm là S = { - 7/6 }.
Chọn đáp án C.
5 tháng 9 2023
a: ĐKXĐ: x>=3
Sửa đề: \(\sqrt{4x-12}-\sqrt{9x-27}+\sqrt{\dfrac{25x-75}{4}}-3=0\)
=>\(2\sqrt{x-3}-3\sqrt{x-3}+\dfrac{5}{2}\sqrt{x-3}-3=0\)
=>\(\dfrac{3}{2}\sqrt{x-3}=3\)
=>\(\sqrt{x-3}=2\)
=>x-3=4
=>x=7(nhận)
b: ĐKXĐ: x>=0
\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< =-\dfrac{3}{4}\)
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}+\dfrac{3}{4}< =0\)
=>\(\dfrac{4\sqrt{x}-8+3\sqrt{x}+3}{4\left(\sqrt{x}+1\right)}< =0\)
=>\(7\sqrt{x}-5< =0\)
=>\(\sqrt{x}< =\dfrac{5}{7}\)
=>0<=x<=25/49
c: ĐKXĐ: x>=5
\(\sqrt{9x-45}-14\sqrt{\dfrac{x-5}{49}}+\dfrac{1}{4}\sqrt{4x-20}=3\)
=>\(3\sqrt{x-5}-14\cdot\dfrac{\sqrt{x-5}}{7}+\dfrac{1}{4}\cdot2\cdot\sqrt{x-5}=3\)
=>\(\dfrac{3}{2}\sqrt{x-5}=3\)
=>\(\sqrt{x-5}=2\)
=>x-5=4
=>x=9(nhận)
DT
1
Nobita Kun
PT
1
28 tháng 8 2019
\(\left(1+\sqrt{5}\right)x+\sqrt{45}=\sqrt{320}\)
\(\Rightarrow x\left(\sqrt{5}+1\right)+3\sqrt{5}-8\sqrt{5}=0\)
\(\Rightarrow x\left(\sqrt{5}+1\right)+3\left(\sqrt{5}+1\right)-8\left(\sqrt{5}+1\right)=5\)
\(\Rightarrow\left(x-5\right)\left(\sqrt{5}+1\right)=5\)
\(\Rightarrow x-5=4-\sqrt{5}\)
\(\Rightarrow x=9-\sqrt{5}\)
PM
2
31 tháng 10 2017
Đặt \(\sqrt[3]{x+45}=a\Rightarrow a^3=x+45\)
\(\sqrt[3]{x-16}=b\Rightarrow b^3=x-16\)
Ta có:\(\hept{\begin{cases}a-b=1\\a^3-b^3=61\end{cases}\Rightarrow\hept{\begin{cases}b=a-1\\\left(a-b\right)^3+3ab\left(a-b\right)=61\end{cases}}}\)
\(\Rightarrow1+3a\left(a-1\right)=61\) (vì a-b=1)
\(\Leftrightarrow a^2-a-20=0\)
\(\Leftrightarrow\left(a-5\right)\left(a+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=5\\a=-4\end{cases}\Rightarrow\orbr{\begin{cases}a^3=125\\a^3=-64\end{cases}\Rightarrow}\orbr{\begin{cases}x=80\\x=-109\end{cases}}}\)
Vậy nghiệm của pt là: x=80;x=-109
24 tháng 8 2021
`sqrt{x-5}+2sqrt{4x-20}-1/2sqrt{9x-45}=12`
Điều kiện:`x>=5`
`pt<=>sqrt{x-5}+2sqrt{4(x-5)}-1/2sqrt{9(x-5)}=12`
`<=>sqrt{x-5}+4sqrt{x-5}-3/2sqrt{x-5}=12`
`<=>7/2sqrt{x-5}=12`
`<=>sqrt{x-5}=24/7`
`<=>x-5=576/49`
`<=>x=821/49(Tmđk)`
Vậy `S={821/49}.`
25 tháng 8 2021
Ta có: \(\sqrt{x-5}+2\sqrt{4x-20}-\dfrac{1}{3}\sqrt{9x-45}=12\)
\(\Leftrightarrow4\sqrt{x-5}=12\)
\(\Leftrightarrow x-5=9\)
hay x=14
\(x=\frac{45}{5396}\)