Giải phương trình
(2x^2-1)3+(2-5x)3=(2x^2-5x+3)3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 6 2023
a: =>|5x-2|=|2x-3|
=>5x-2=2x-3 hoặc 5x-2=-2x+3
=>3x=-1 hoặc 7x=5
=>x=5/7 hoặc x=-1/3
b: =>|5x-2|-|2x+2|=3x+5
TH1 x<-1
PT sẽ là 2-5x+2x+2=3x+5
=>-3x+4=3x+5
=>-6x=1
=>x=-1/6(loại)
TH2: -1<=x<2/5
Pt sẽ là 2-5x-2x-2=3x+5
=>-7x=3x+5
=>-4x=5
=>x=-5/4(loại)
Th3: x>=2/5
PT sẽ là 5x-2-2x-2=3x+5
=>3x-4=3x+5
=>0x=9(loại)
KS
1
NM
Nguyễn Minh Quang
Giáo viên
1 tháng 3 2021
ta có
\(\left(5x^2+2x-1\right)-\left(2x-1\right)\sqrt{5x^2+2x-1}-\left(4x+2\right)=0\)
Đặt \(\sqrt{5x^2+2x-1}=a\ge0\Rightarrow a^2-\left(2x-1\right)a-\left(4a+2\right)=0\)
\(\Rightarrow\Delta=\left(2x-1\right)^2+4\left(4x+2\right)=4x^2+12x+9=\left(2x+3\right)^2\)
\(\Rightarrow\orbr{\begin{cases}a=\frac{2x-1+2x+3}{2}=1\\a=\frac{2x-1-2x-3}{2}=-2\text{ (Loại)}\end{cases}\Rightarrow5x^2+2x-1=1\Rightarrow x=\frac{-1\pm\sqrt{11}}{5}}\)
CM
21 tháng 1 2019
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
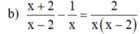
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
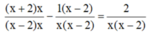
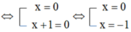
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
PN
9 tháng 5 2021
a,\(2x+5=2-x\)
\(< =>2x+x+5-2=0\)
\(< =>3x+3=0\)
\(< =>x=-1\)
b, \(/x-7/=2x+3\)
Với \(x\ge7\)thì \(PT< =>x-7=2x+3\)
\(< =>2x-x+3+7=0\)
\(< =>x+10=0< =>x=-10\)( lọai )
Với \(x< 7\)thì \(PT< =>7-x=2x+3\)
\(< =>2x+x+3-7=0\)
\(< =>3x-4=0< =>x=\frac{4}{3}\) ( loại )
PN
9 tháng 5 2021
c,\(\frac{4}{x+2}-\frac{4x-6}{4x-x^3}=\frac{x-3}{x\left(x-2\right)}\left(đk:x\ne-2;0;2\right)\)
\(< =>\frac{4x\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}+\frac{4x-6}{x\left(x-2\right)\left(2+x\right)}=\frac{\left(x-3\right)\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}\)
\(< =>4x^2-8x+4x-6=x^2-x-6\)
\(< =>4x^2-x^2-4x+x-6+6=0\)
\(< =>3x^2-3x=0< =>3x\left(x-1\right)=0< =>\orbr{\begin{cases}x=0\left(loai\right)\\x=1\left(tm\right)\end{cases}}\)
Ok mình sẽ giúp bạn!!
(2x2+1)3 + (2-5x)3 = (2x2-5x+3)3
<=> (2x2+1)3 +(2-5x)3 - (2x2-5x+3)3 =0
<=> (2x2+1)3+(2-5x)3+(-2x2+5x-3)3 =0 ( Chỉ có mũ lẽ thì mới đổi dấu được nhé ) (5)
Đặt a=2x2+1 ; b=2-5x ; c=-2x2+5x-3 (4)
=> a+b+c=2x2+1+2-5x-2x2+5x-3=0 => a+b=-c ; b+c=-a ; a+c=-b (2)
Ta có
a+b+c =0
<=>(a+b+c)3=0
<=> (a+b)3 +3(a+b)2 +3(a+b)c2+c3=0
<=>a3+b3+3ab(a+b) +3(a+b)2c+3(a+b)c2+c3=0
<=>a3+b3+c3 +3(a+b)[ab+(a+b)c +c2]=0
<=>a3+b3+c3 + 3(a+b)(ab+ac+bc+c2) =0
<=>a3+b3+c3 +3(a+b)[a(b+c)+c(b+c)]=0
<=>a3+b3+c3 +3(a+b)(b+c)(a+c) =0 (1)
Thay (2) vào (1) ta có:
a3+b3+c3+ 3(-c)(-a)(-b) =0
<=> a3+b3+c3-3abc=0
<=> a3+b3+c3=3abc (3)
Thay(4) vào (3) => (2x2+1)3+(2-5x)3+(-2x2+5x-3)3 = 3(2x2+1)(2-5x)(-2x2+5x-3) (6)
Từ (5)và(6) ta có
3(2x2+1)(2-5x)(-2x2+5x-3)=0
<=> (2x2+1)(2-5x)(-2x2+2x+3x-3)=0
<=>(2x2+1)(2-5x)[-2x(x-1)+3(x-1)]=0
<=>(2x2+1)(2-5x)(3-2x)(x-1)=0
Mà 2x2+1 >0 với mọi x thuộc R
=> 2-5x=0 <=> x=2/5
hoặc 3-2x=0 <=> x=3/2
hoặc x-1=0 <=> x=1
Vậy .....
mk nhé!!
Bạn ơi!! Bạn xem lại đề bài xem ở kia là (2x2-1)3 hay là (2x2+1)3