cho hình thang vuông ABCD có góc A=90;góc B=90;AB=BC=1/2 AD.E là trung điểm của AD. a)tứ giác ANCE là hình gì?Vì sao? b) kẻ AH vuông góc BD(H thuộc BD).Gọi M,N lần lượt là trung điểm của HD,HA. tg BCMN là hình bình hành c)AM vuông góc MC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2018
a, Bạn chứng minh được \(\Delta ABD\infty\Delta BDC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow AB.DC=BD^2\Rightarrow2.8=BD^2\Rightarrow BD^2=16\Rightarrow BD=4\left(cm\right)\)(vì AB = 2cm , CD = 8 cm)
Ta có: \(\frac{BD}{CD}=\frac{4}{8}=\frac{1}{2}\)
Xét tam giác BDC vuông tại B có: BD = 1/2 CD nên \(\widehat{C}=30^0\)
ABCD là hình thang vuông(gt) \(\Rightarrow AB//CD\)
\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\) ( 2 góc trong cùng phía)
\(\Rightarrow\widehat{ABC}+30^0=180^0\) (do góc C = 30 độ)
\(\Rightarrow\widehat{ABC}=150^0\)
b, Áp dụng định lí Pitago vào tam giác ABD vuông tại A, tính được: \(AD=\sqrt{12}\left(cm\right)\)
Diện tích hình thang ABCD là:
\(\frac{\left(2+8\right).\sqrt{12}}{2}=5\sqrt{12}\left(cm^2\right)\)
Chúc bạn học tốt.
16 tháng 7 2021
Tam giác ACD vuông tại C có góc CAD = góc ABC = 60 độ (cùng phụ với CAB)
=> AC = 2AD
Áp dụng Pytago ta có:
AC2 = AD2 + DC2
<=> 4AD2 = AD2 + 900
<=> AD2 = 300
<=> AD=10√3AD=103
Kẻ CH vuông với AB
AHCD là hình chữ nhật (có góc A=D=H = 900)
=> AH = CD = 30; CH = AD = 10√3103
Tgiac ACB vuông tại C, ta có:
CH2 =HA.HB
=> HB=CH2/ H A=10
=> AB = AH + HB = 40
diện tích hình thang ABCD=1/2CH.(AB+CD)=350√3
12 tháng 8 2021
\(2,\)
A B H C D
Kẻ BH vuông góc với CD tại H
Xét hai tam giác BDH và BCH:
+) BH là cạnh chung
+) Góc BHD = góc BHC = 90 độ
+) DH = CH
=> Tam giác BDH = tam giác HCH (c.g.c)
=> BD = BC
Khác: DC = BC
=> BC = CD = DB => Tam giác BCD đều => Góc C = 60 độ
Mà: AB // CD => Góc B + góc C = 180 độ => Góc B = góc ABC = 180 độ - 60 độ = 120 độ
TD
2
LA
23 tháng 6 2017
dùng tỉ số lượng giác lần lượt tính được AD= \(10\sqrt{3}\) cm;AC= \(20\sqrt{3}\) cm;AB=20cm
do đó S hình thang\(=\frac{\left(ab+cd\right)\cdot ad}{2}=\frac{\left(20+30\right)\cdot10\sqrt{3}}{2}=\frac{500\sqrt{3}}{2}cm^2\)
Vậy....
CM
8 tháng 5 2018
Đáp án cần chọn là: D
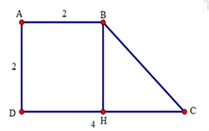
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .
14 tháng 7 2023
a: Kẻ BH vuông góc CD
Xét tứ giác ABHD có
góc BAD=góc ADH=góc BHD=90 độ
AB=AD
=>ABHD là hình vuông
=>BH=HD=AB=DC/2
=>góc BDH=45 độ
DH=DC/2
=>H là trung điểm của DC
Xét ΔBDC có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBDC cân tại B
=>góc C=45 độ
=>góc ABC=135 độ
c: DC=2*3=6cm
AD=AB=3cm
BC=căn 3^2+3^2=3*căn 2cm
C=6+3+3+3căn 2=12+3căn 2(cm)
b: Ta có: \(AE=ED=\dfrac{1}{2}AD\)
mà \(AB=BC=\dfrac{AD}{2}\)
nên AE=ED=AB=BC
Xét tứ giác AECB có
AE//CB
AE=CB
Do đó: AECB là hình bình hành
mà \(\widehat{EAB}=90^0\)
nên AECB là hình chữ nhật
mà AE=AB
nên AECB là hình vuông
Xét ΔHAD có
N là trung điểm của AH
M là trung điểm của HD
Do đó: MN là đường trung bình của ΔHAD
Suy ra: MN//AD và \(MN=\dfrac{AD}{2}\)
mà \(AE=BC=\dfrac{AD}{2}\) và AD//BC
nên MN//BC và MN=BC
Xét tứ giác BCMN có
MN//BC
MN=BC
Do đó: BCMN là hình bình hành