Cho hình thang cân ABCD có đáy CD=14cm;cạnh bên AD=căn 32 cmvà góc ADC= 45 độ. Diện tích hình thang cân ABCD là .....cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

hình tự vẽ nha bạn
kẻ đường cao AH=> tam giác AHD vuông cân tại H
=> AH=DH
áp dụng Pitago => AH=DH=4cm
tương tự kẻ đường caoBK=> tam giác BKC vuông cân tại K
=> BK=KC
áp dụng Pitago =>BK=KC=4cm
ta có AB//DC ,BK vuông góc với DC=> AB vuông góc với BK
tứ giác ABKH có góc ABK=góc BKH=góc KHA=90 độ
=> T/g ABKH là hcn=> AB=HK=CD-(DH+KC)=14-(4+4)=6m
S ABCD=(AB+CD).AH:2=(6+14).4:2=40 cm vuông
Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.

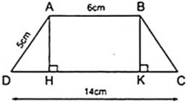
Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có: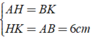
Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:
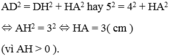
Vậy chiều cao của hình thang cân là 3cm.

kẻ 1 đg vuông góc từ B cắt DC tại K
xét tg ADH và tg BCK :
góc AHD= góc BKC ( = 90 độ )
AD= BC ( gt )
góc ADH= góc BCK ( gt )
=> tg ADH= tg BCK ( ch- gn)
=> DH= KC ( 2 cạnh t/ứ ) ( 1)
vì AB song song DC=> ABKD là hcn ( tự chứng minh)
=> AB=Dk= 8 cm
=> DH= KC= (DC-DK ) :2= 3 cm
áp dụng đlí pi-ta-go cho tg ADH vuông ở H :
AH2+DH2= AD2
TS : AH2= 52-32
=> AH = 4 cm
mk nghĩ 20 chớ?
Minh Triều pn ko chia 2 à?