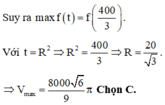Cho hình vuông ABCD nội tiếp đường tròn(O;R).MN là đường kính bất kì.CMR: MA²+MB²+MC²+MD²=8R²
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 6 2018
Đáp án A
Gọi O là giao điểm của AC và BD. Khi đó, đường tròn tâm O bán kính R = a/2 là đường tròn nội tiếp hình vuông ABCD.
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên đường tròn tiếp xúc với các cạnh của hình vuông.
Suy ra: AB; BC; CD và DA là các tiếp tuyến của đường tròn (O).
CM
31 tháng 3 2019
Đáp án C
Gọi cạnh của hình lập phương bằng a
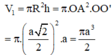
(R là bán kính đường tròn ngoại tiếp hình vuông ABCD)
Thể tích
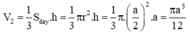
(r là bán kính đường tròn nội tiếp hình vuông ABCD)
29 tháng 12 2023
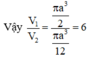
Ta có: ΔBAO vuông tại A
=>ΔBAO nội tiếp đường tròn đường kính BO
=>A nằm trên đường tròn đường kính BO(1)
Ta có: ΔBMO vuông tại M
=>ΔBMO nội tiếp đường tròn đường kính BO
=>M nằm trên đường tròn đường kính BO(2)
Từ (1),(2) suy ra A,B,M,O cùng thuộc đường tròn đường kính BO
CM
20 tháng 1 2017
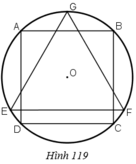
Dựng GH vuông góc EF.
Khi hình vẽ quay quanh trục GO thì:
Ta có:
AB = BC 
Thể tích hình trụ sinh ra bởi hình vuông ABCD là:
Thể tích hình nón:
