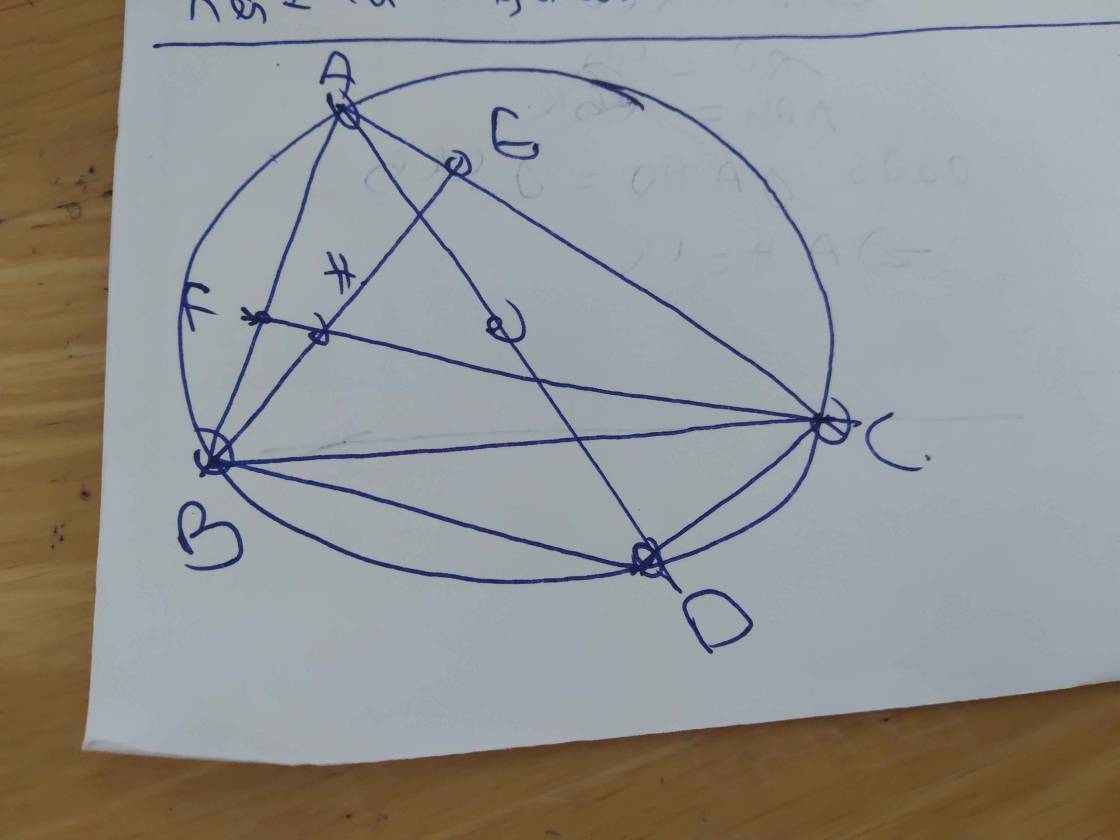
1. Cho △ABC nhọn nội tiếp đường tròn (O;R) đường cao AD, tia AD cắt đường tròn (O) tại M. Vẽ ME ⊥ AC tại E
a) Chứng minh tứ giác MDEC nội tiếp và AD.AM=AE.AC
b) Gọi H là điểm đối xứng của M qua BC. Tia BH cắt AC tại S. Chứng minh AH.AD=AS.AC
c) Cho BC = R√2. Tính khoảng cách từ tâm O đến BC theo R
2. Một chiếc thuyền đi từ vị trí A bên bờ sông này sang vị trí B bên bờ bên kia, AB vuông góc với hai bờ sông. Do nước chảy nên thuyền đã đi lệch một góc 200 và đến vị trí C bên bờ bên kia. Biết khoảng cách giữa hai bờ là 160m. Tính khoảng cách BC (làm tròn đến chữ số thập phân thứ nhất)
3. Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy C (AC>R). Qua C kẻ đường thẳng d⊥CA. Lấy M ∈ (O) sao cho AM=\(\frac{R}{2}\). Tia BM cắt d tại P, tia CM cắt đường tròn tại N, PA cắt đường tròn tại Q
a) Chứng minh tứ giác ACPM nội tiếp
b) NQ // PC
c) Tính thể tích hình tạo thành khi quay tam giác MAB một vòng quanh AM theo R
d) Gọi H là giao của QN và AB, E là giao của MB và QN, AE cắt đường trong tại K. Tính giá trị biểu thức AE.AK + BE.BM theo R
4. Một cầu thang có 20 bậc. Kích thước mỗi bậc rộng 20cm, cao 25cm. Hãy tính khoảng cách từ chân cầu thang đến đầu cầu thang