Cho nửa (O;R) , đường kính AB, OK vuông góc với AB. Trên cung KB lấy M. Trên tia AM lấy N sao cho AN=MB. Kẻ dây BP song song với KM . AP cắt BM tại Q. E là giao của BP và AM. CMR : AM.BE=AN.AQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
Xét (O) có
DC,DA là tiếp tuyến
Do đó: DC=DA
Xét (O)có
EC,EB là tiếp tuyến
Do đó: EC=EB
DC+CE=DE
mà DC=DA và EC=EB
nên DA+EB=DE
b: Xét tứ giác DAOC có \(\widehat{DAO}+\widehat{DCO}=90^0+90^0=180^0\)
=>DAOC là tứ giác nội tiếp
=>D,A,O,C cùng thuộc một đường tròn
Xét ΔOAC có OA=OC=R
nên ΔOAC cân tại O
ADCO là tứ giác nội tiếp
=>\(\widehat{ADO}=\widehat{ACO}\)
mà \(\widehat{ACO}=\widehat{OAC}\)(ΔOAC cân tại O)
nên \(\widehat{ADO}=\widehat{OAC}=\widehat{CAB}\)

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
góc DMO+góc DBO=180 độ
=>DMOB nội tiếp
b: Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc DOC=1/2*180=90 độ
Xét ΔDOC vuông tại O có OM là đường cao
nên CM*MD=OM^2
=>AC*BD=R^2

a.
Do AD là tiếp tuyến tại A \(\Rightarrow\widehat{OAD}=90^0\)
\(\Rightarrow\) 3 điểm O, A, D thuộc đường tròn đường kính OD (1)
BD là tiếp tuyến tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) 3 điểm O, B, D thuộc đường tròn đường kính OD (2)
(1);(2) \(\Rightarrow\) 4 điểm A, D, B, O cùng thuộc đường tròn đường kính OD
b.
Do D là giao điểm 2 tiếp tuyến tại A và B, theo t/c hai tiếp tuyến cắt nhau
\(\Rightarrow DA=DB\)
Mà \(OA=OB=R\)
\(\Rightarrow OD\) là trung trực của AB \(\Rightarrow OD\perp AB\) (3)
BC là đường kính và A thuộc đường tròn nên \(\widehat{BAC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow BA\perp CA\) (4)
(3);(4) \(\Rightarrow OD||CA\) (cùng vuông góc AB) hay \(OD||CE\)
Áp dụng hệ thức lượng trong tam giác vuông BCE với đường cao BA ứng với cạnh huyền:
\(BC^2=CA.CE\Rightarrow\left(2R\right)^2=CA.CE\)
\(\Rightarrow CA.CE=4R^2\)
Em kiểm tra lại đề bài, đoạn này là sao nhỉ: "Tiếp tuyến tại 4 của (O) "

a: Xét tứ giác ADBO có
\(\widehat{DBO}+\widehat{DAO}=90^0+90^0=180^0\)
=>ADBO là tứ giác nội tiếp
=>A,D,B,O cùng thuộc một đường tròn
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>BA\(\perp\)AC tại A
=>BA\(\perp\)CE tại A
Xét (O) có
DA,DB là các tiếp tuyến
DO đó: DA=DB
=>D nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OD là đường trung trực của AB
=>OD\(\perp\)AB
Ta có: OD\(\perp\)AB
CE\(\perp\)AB
Do đó: OD//CE
Xét ΔEBC vuông tại B có BA là đường cao
nên \(CA\cdot CE=CB^2\)
=>\(CA\cdot CE=\left(2R\right)^2=4R^2\)

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔABD vuông tại A có AC là đường cao
nên \(AD^2=DB\cdot DC\)

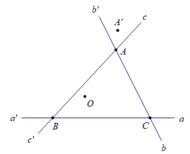
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.
góc PAM=góc PBM
=>góc QAM=góc EBM
=>ΔAQM đồng dạng vơi ΔBEM
=>AQ/BE=AM/BM=AM/AN
=>AQ*AN=BE*AM