tam giác MNI cân tại M.có NE;NI là các đường chéo phân giac lần lượt của góc N, góc I. C/m: a,tứ giác EFNI là hình thang cân b.EF=EI=FN c, Nếu gócM=44. Tính các góc của tứ giác EFNI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔDEC có
I là trung điểm của DE
N là trung điểm của DC
Do đó: NI là đường trung bình của ΔDEC
Suy ra: \(NI=\dfrac{EC}{2}\)
hay \(NI=\dfrac{BD}{2}\left(1\right)\)
Xét ΔDBC có
N là trung điểm của DC
M là trung điểm của BC
Do đó: NM là đường trung bình của ΔDCB
Suy ra: \(NM=\dfrac{DB}{2}\left(2\right)\)
Từ (1) và (2) suy ra NI=NM
Xét ΔNIM có NI=NM
nên ΔNIM cân tại N

Dễ thấy AB,AC là đường trung bình tam giác NMI
Do đó \(AC=\dfrac{1}{2}MI=MB\) (B là trung điểm MI) và AC//MI hay AC//MB
Do đó AMBC là hbh (1)
Mà AB là đtb tg NMI nên AB//NI
Mà tg MNI cân tại M nên MC là trung tuyến cx là đường cao
Do đó \(MC\perp NI\Rightarrow MC\perp AB\left(2\right)\)
Từ (1)(2) ta được AMBC là hình thoi

Bài 4:
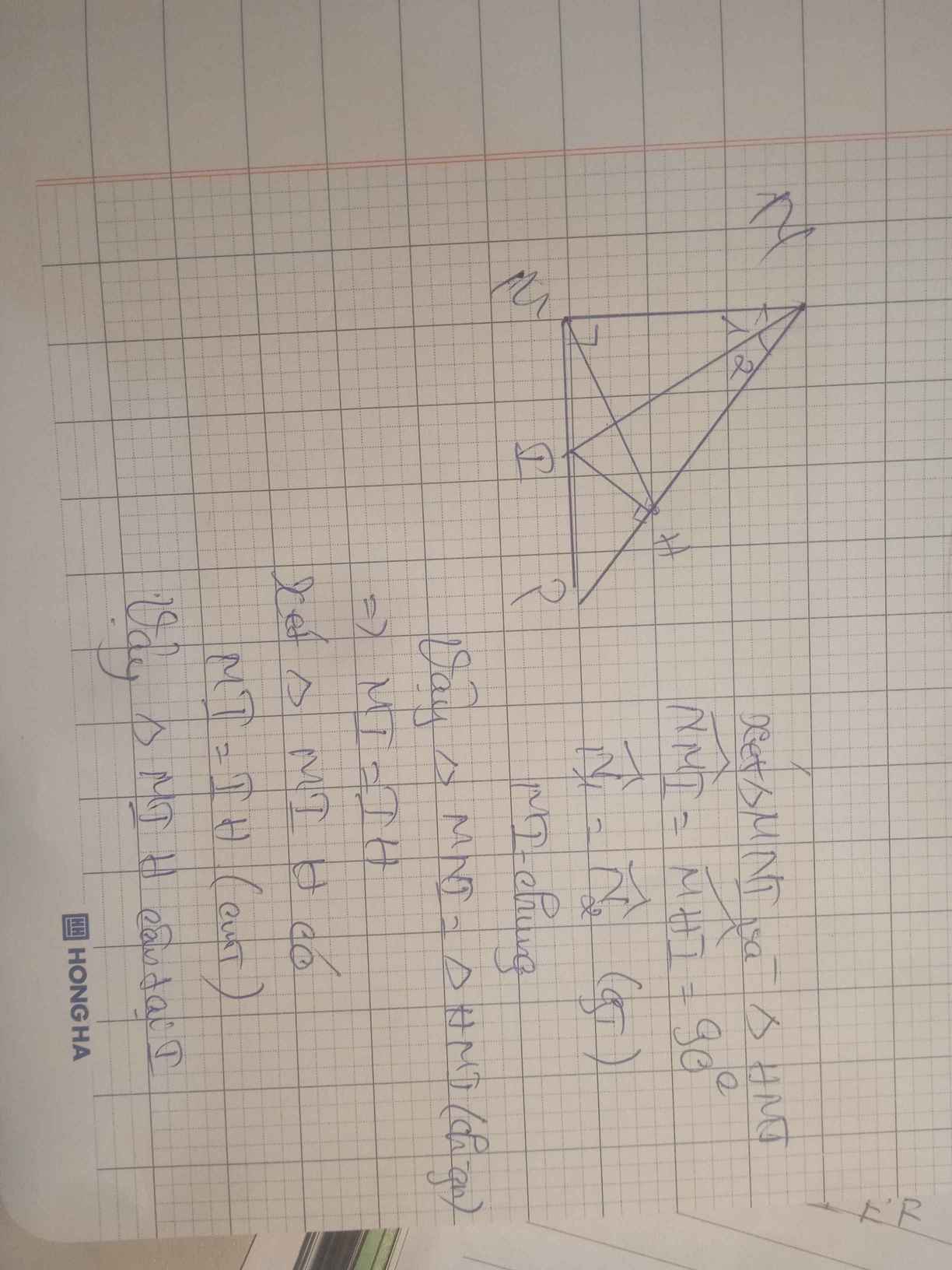
a: Xét ΔBHC vuông tại H và ΔCKB vuông tại K có
BC chung
\(\widehat{HCB}=\widehat{KBC}\)
Do đó: ΔBHC=ΔCKB
b: Ta có: ΔBHC=ΔCKB
nên HC=KB(hai cạnh tương ứng)
Ta có: AK+KB=AB
AH+HC=AC
mà KB=HC
và AB=AC
nên AK=AH
c: Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\)
Do đó: KH//BC
Xét tứ giác BKHC có KH//BC
nên BKHC là hình thang
mà BH=CK
nên BKHC là hình thang cân

a: Xét ΔMEN và ΔMFP co
ME=MF
góc M chung
MN=NP
=>ΔMEN=ΔMFP
=>EN=FP
b: Xét ΔFNP và ΔEPN có
FN=EP
NP chung
FP=EN
=>ΔFNP=ΔEPN
=>góc ONP=góc OPN
=>ON=OP
Xét ΔMON và ΔMOP có
MO chung
ON=OP
MN=MP
=>ΔMON=ΔMOP
=>góc NMO=góc PMO
=>MO là phân giác của góc NMP