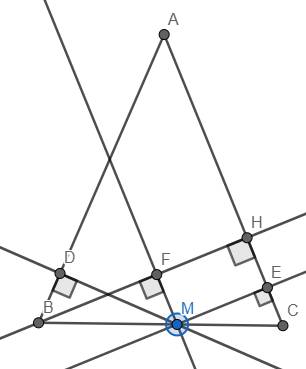
Bài 1: cho \(\Delta\) ABC cân ở A, điểm M thuộc BC, Kẻ ME \(\perp\) AC

NM

Nguyễn Mai Trang b

4 tháng 2 2017

Bài 1: cho \(\Delta\) ABC cân ở A, điểm M thuộc BC, Kẻ ME \(\perp\) AC ;MF\(\perp\) AB A, chứng minh: góc BMF= góc CME B, Đường thẳng đi qua M \(\perp\) BC cắt đường thẳng AB,AC là N,Q Chứng minh: MQ là tia phân giác góc EMF C,AQ=AN D,kẻ AH // BC .Chứng minh:H là trung điểm Q,N Bài 2: Cho\(\Delta\) ABC cân tại A: Trên cạnh BC LẤY D.Trên tia đối CA lấyE sao choBD=CE;I là trung điểm MC a,Chứng minh: D;I;E thẳng hàng...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

0

TD

Trần Đức Vinh

18 tháng 8 2023 - olm

Cho \(\Delta ABC\) cân tại A,đường cao BH trên đáy BC lấy điểm M,vẽ \(MD\perp AB,ME\perp AC,MF\perp BH\). a) Chứng minh ME = HF b) \(\Delta DBM=\Delta FMB\) c)Khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi. d)Trên tia đối của tia CA lấy điểm K sao cho KC = EH.Chứng minhtrung điểm của KD nằm trên cạnh...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

2

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

18 tháng 8 2023

A B C H D E F M K N

a/

\(BH\perp AC\Rightarrow HF\perp AC;ME\perp AC\) => ME//HF

\(AC\perp AB\Rightarrow EH\perp HF;MF\perp BH\Rightarrow MF\perp HF\) => EH//MF

=> MEHF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => ME=HF (cạnh đối hbh)

b/

\(\widehat{BMD}+\widehat{ABC}=90^o\)

\(\widehat{CME}+\widehat{ACB}=90^o\)

\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{BMD}=\widehat{CME}\)

Mà \(\widehat{CME}=\widehat{CBH}\) (góc đồng vị)

\(\Rightarrow\widehat{BMD}=\widehat{CBH}\)

Xét tg vuông DBM và tg vuông FMB có

\(\widehat{BMD}=\widehat{CBH}\)

BM chung

=> tg DBM = tg FMB (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)

c/

Ta có ME = HF (cmt)

tg DBM = tg FMB (cmt) => MD = BF

=> MD+ME=BF+HF=BH không đổi

d/

Từ D dựng đt // AC cắt BC tại N

\(\Rightarrow\widehat{BND}=\widehat{ACB}\) Góc đồng vị)

\(\widehat{ABC}=\widehat{ACB}\)

=> \(\widehat{BND}=\widehat{ABC}\) => tg DBN cân tại D => BD=ND (1)

tg DBM = tg FMB (cmt) => BD=MF (2)

Mà MF = EH (cạnh đối hbh) (3)

Mà EH = KC (4)

Từ (1) (2) (3) (4) => ND = KC

Mà ND//AC => ND//KC

=> DEKN là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)

Mà DK và NC là hai đường chéo của hbh cắt nhau tại trung điểm mỗi đường => trung điểm của KD nằm trên NC mà NC thuộc BC => trung điểm KD nằm trên BC

Đúng(0)

WT

when the imposter is sus

21 tháng 8 2023

a) Vẽ MH, rõ ràng HEMF có tổng số đo của 4 góc là 360^o (vì tổng số đo của 4 góc đó là tổng số đo của các góc của các tam giác FMH và EMH)

Mà theo giả thuyết \(MD\perp AB\), \(ME\perp AC\) và \(MF\perp BH\) nên \(MF\perp ME\). Suy ra HEMF là hình chữ nhật, từ đó ME = HF.

b) Ta có \(\widehat{ABM}=\widehat{ACM}\) (vì tam giác ABC cân tại A) và \(\widehat{FMB}=\widehat{ACM}\) (vì hai góc đồng vị và AC//MF vì \(ME\perp AC\) và \(MF\perp ME\)), suy ra \(\widehat{ABM}=\widehat{FMB}\).

Xét tam giác DBM vuông tại D và FMB vuông tại F có BM là cạnh chung và \(\widehat{ABM}=\widehat{FMB}\), suy ra ΔDBM = ΔFMB (cạnh huyền - góc nhọn)

c) Từ a) và b) suy ra MD = BF, MD + ME = BF + FH = BH. Vậy khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.

Đúng(0)

RH

RF huy

18 tháng 3 2021 - olm

cho tam giác ABC cân tại A. Gọi M là trung điểm của BC

a C/M: \(\Delta ABM=\Delta ACM\)và \(AM\perp BC\)

b, Kẻ \(ME\perp AB\) tại E, \(ME\perp AC\)tại F, C/m: \(\Delta EMF\)cân tại M.

c, C/M: EF//BC

#Hỏi cộng đồng OLM #Toán lớp 7

1

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

18 tháng 3 2021

a/

Xét tg ABM và tg ACM có

MB=MC (đề bài)

AB=AC (Do tg ABC cân tại A)

\(\widehat{ABC}=\widehat{ACB}\) (Do tg ABC cân tại A)

=> tg ABM=tg ACM (c.g.c)

Ta có MB=MC => AM là trung tuyến của tg ABC => \(AM\perp BC\) (trong tg cân đường trung tuyến đồng thời là đường cao)

b/

Xét tg vuông BME và tg vuông CMF có

MB=MC

\(\widehat{ABC}=\widehat{ACB}\)

=> tg BME = tg CMF (hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => ME=MF => tg EMF cân tại M

c/

Do \(AM\perp BC\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)

Do tg BME = tg CMF \(\Rightarrow\widehat{BME}=\widehat{CME}\)

\(\Rightarrow\widehat{AME}=\widehat{AMF}\) (cungf phụ với \(\widehat{BME}\) = \(\widehat{CMF}\) )

=> AM là phân giác của \(\widehat{FME}\Rightarrow AM\perp EF\) (Trong tg can EMF đường phân giác đồng thời là đường cao)

Mà \(AM\perp BC\)

=> EF//BC (cùng vuông góc với AM)

Đúng(0)

RH

RF huy

15 tháng 3 2021 - olm

cho tam giác ABC cân tại A. Gọi M là trung điểm của BC.

a, C/m \(\Delta ABM=\Delta ACM\)và \(AM\perp BC\)

b, kẻ \(ME\perp AB\)tại E, \(ME\perp AC\)tại F. C/m \(\Delta EMF\)cân tại M

c, C/m EF//BC

#Hỏi cộng đồng OLM #Toán lớp 7

0

NT

Nguyễn Thị Thu Huyền

28 tháng 12 2023 - olm

Cho \(\Delta ABC\) cân tại A, lấy điểm M là trung điểm của cạnh BC. Trên tia đối của MA lấy điểm D sao cho MA = MD Chứng minh: a) \(\Delta AMB\) và \(\Delta DMC\) b) AC // BD c) Kẻ AH \(\perp\) BC, DK \(\perp\) BC ( H, K \(\in\) BC ) Chứng minh BK =...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

2

NT

Nguyễn Thị Hoài An

28 tháng 12 2023

δγΣαγηθλΣϕΩβΔ

Đúng(0)

5P

59 Phan Mỹ Vân

28 tháng 12 2023

Xét △AMD và △DMC

AB=AC(giả thuyết)

Cạnh AM là cạnh chung

BM= CM ( M là trung điểm của cạnh BC)

=> △AMD=△DMC

Sorry bạn nhé mk chỉ bt làm câu a thui ☹

Đúng(1)

TT

Tiểu Thư họ Nguyễn

18 tháng 2 2017

Cho Δ ABC vuông tại A. Đường cao AH. Kẻ HD ⊥ AB, HE ⊥ AC. Gọi O là trung điểm của AH.
Kẻ AM ⊥ DE (M thuộc BC). Chứng minh M là trung điểm của BC

#Hỏi cộng đồng OLM #Toán lớp 7

1

LQ

Lê Quỳnh Trang

18 tháng 2 2017

bn tham khảo ở đây nha:http://text.123doc.org/document/658748-6-bai-toan-hinh-4-de-thi-ki-i-toan-8.htm

Đúng(0)

AT

Ánh Tuyết

13 tháng 11 2021

Cho \(\Delta\)ABC \(\perp\) tại A có AB < AC, M là trung điểm của BC. Kẻ ME \(\perp\) AB ( E \(\in\) AB ) , kẻ MF \(\perp\) AC ( F \(\in\) AC )a) Tứ giác AEMF là hình gì? Vì sao?b) chứng minh EF = 1/2 BCc) Gọi K là chân đường vuông góc kẻ từ A đến BC. Chứng minh rằng tứ giác EKMF là hình thang...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 11 2021

a: Xét tứ giác AEMF có

\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)

Do đó: AEMF là hình chữ nhật

Đúng(0)

DT

Đậu Thị Khánh Huyền

6 tháng 1 2018

Cho \(\Delta ABC\); AB = AC, M là trung điểm BC. Kẻ \(MD\perp AB,ME\perp AC\). CMR:

a) MD = ME

b) DE // BC

#Hỏi cộng đồng OLM #Toán lớp 7

1

NT

Nguyễn Thanh Hằng

6 tháng 1 2018

A B C M D E

a/ \(\Delta ABC\) có : AB = AC

\(\Leftrightarrow\Delta ABC\) cân tại A

\(\Leftrightarrow\widehat{B}=\widehat{C}\) (2 góc ở đáy)

Xét \(\Delta BDM;\Delta CEM\) có :

\(\left\{{}\begin{matrix}\widehat{BDM}=\widehat{CEM}=90^0\\MB=MC\\\widehat{B}=\widehat{C}\end{matrix}\right.\)

\(\Leftrightarrow\Delta BDM=\Delta CEM\left(ch-gn\right)\)

\(\Leftrightarrow MD=ME\)

Đúng(0)

QN

Quỳnh Như

2 tháng 3 2022

Cho tam giác ABC cân tại A .Gọi M là trung điểm của BC

a)C/m:△ABM=△ACM và AM\(\perp\)BC

b) Kẻ ME \(\perp\)AB tại E,ME\(\perp\)AC tại F. C/m △EMF cân tại M

c) C/m: EF//BC

#Hỏi cộng đồng OLM #Toán lớp 7

1

VV

Vinh Vu hoang

2 tháng 3 2022

Vì △ABC cân tại A

=> ABC = ACB

Xét △BDM vuông tại D và △CEM vuông tại E

Có: BM = CM (gt)

DBM = ECM

=> △BDM = △CEM (ch-gn)

=> DM = EM (2 cạnh tương ứng)

Xét △AMD vuông tại D và △AME vuông tại E

Có: DM = ME (cmt)

AM là cạnh chung

=> △AMD = △AME (ch-cgv)

=> AD = AE (2 cạnh tương ứng)

Xét △ADE có AD = AE

=> △ADE cân tại A

=> ADC = (180^o - A) : 2 (1)

Vì △ABC cân tại A

=> ABC = (180^o - A) : 2 (2)

Từ (1), (2) => ADC = ABC

Mà 2 góc này nằm ở vị trí đồng vị

=> DE // BC (dhnb)

Đúng(4)

VN

Võ Nguyễn Nhật Minh

9 tháng 2 2018

Cho Δ ABC cân tại A, lấy điểm M là trung điểm của đoạn BC

a) Chứng minh: ΔABM = ΔACM

b) Vẽ MD ⊥ AB (D thuộc AB) và kẻ ME ⊥ AC (E thuộc AC)

Chứng minh : △ADE cân và DE //BC

c) Qua D vẽ đường thẳng // với AM, đường thẳng này cắt EM tại K

Chứng minh: EK = 2MD

#Hỏi cộng đồng OLM #Toán lớp 7

1

NT

nguyen thi vang

9 tháng 2 2018

A B C D E M K

a) Xét \(\Delta ABM,\Delta ACM\) có:

\(AB=AC\) (\(\Delta ABC\) cân tại A)

\(BM=MC\) (M là trung điểm của BC)

\(AM:Chung\)

=> \(\Delta ABM=\Delta ACM\left(c.c.c\right)\) (*)

b) Xét \(\Delta BDM,\Delta CEM\) có :

\(\widehat{DBM}=\widehat{ECM}\) (Tam giác ACB cân tại A)

\(BM=MC\) (M là trung điểm của BC)

\(\widehat{BDM}=\widehat{CEM}\left(=90^o\right)\)

=> \(\Delta BDM=\Delta CEM\) (cạnh huyền - góc nhọn)

=> \(DM=EC\) (2 cạnh tương ứng)

=> \(\widehat{DAM}=\widehat{EAM}\)

Xét \(\Delta ADM,\Delta AEM\) có :

\(\widehat{ADM}=\widehat{AEM}\left(=90^{^o}\right)\)

\(DM=CE\left(cmt\right)\)

\(\widehat{DAM}=\widehat{EAM}\) (từ *)

=> \(\Delta ADM=\Delta AEM\left(g.c.g\right)\)

=> AD = AE (2 cạnh tương ứng)

Do đó : \(\Delta ADE\) cân tại A => đpcm

Xét \(\Delta ADE\) cân tại A có :

\(\widehat{ADE}=\dfrac{180^{^O}-\widehat{A}}{2}\left(1\right)\)

Xét \(\Delta ABC\) cân tại A(gt) có :

\(\widehat{ABC}=\dfrac{180^{^O}-\widehat{A}}{2}\left(2\right)\)

Từ (1) và (2) => \(\widehat{ADE}=\widehat{ABC}\left(=\dfrac{180^O-\widehat{A}}{2}\right)\)

Mà thấy : 2 góc này ở vị trí đồng vị

Do đó : \(DE//BC\left(đpcm\right)\)

c) Ta có : \(DM=EM\left(\Delta BDM=\Delta CEM-cmt\right)\) (3)

Ta dễ dàng chứng minh được : \(\Delta CEM=\Delta KBM\)

Từ đó suy ra : KM = ME (2 cạnh tương ứng)

\(\Leftrightarrow EK=2EM\) (4)

Từ (3) và (4) => \(EK=2MD\)

=> đpcm.

Đúng(0)

MC

Mina Cadie

27 tháng 12 2015 - olm

Cho tam giác ABC cân tại A, AB=AC=5cm. Gọi M là 1 điểm thuộc BC. Qua M kẻ đường thẳng // AB,AC cắt AB ở F, AB cắt AC ở E. Tính ME+MF

#Hỏi cộng đồng OLM #Toán lớp 7

1

DT

Đào Thu Ngọc

27 tháng 12 2015

tick cho mk đi thì mk làm

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP