Cho hình vẽ sau : Biết A = 30 độ ; B = 45 độ , AOB = 75 độ
Chứng minh rằng : a//b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ Oc//a thì Oc//b
\(\Rightarrow\widehat{AOB}=\widehat{AOc}+\widehat{BOc}=\widehat{OAa}+\widehat{OBb}=30^0+40^0=70^0\)

A B O a y b 30 45
(ý bn cá hình nó vẽ như trên đúng ko)
Kẻ y // a (1)
=> góc CAO = góc AOy ( so le trong)
=> góc AOy = 30
Ta có góc AOB = góc AOy + góc yOB
=> góc yOB = góc AOB - góc AOy = 75 - 30 = 45
=> góc yOB = góc OBD( = 45 )
Mà 2 góc nằm ở vị trí so le trong
=> y//b (2)
Từ (1) và (2) => a//b
Làm bài như con kặc ấy, OBD mày lấy đâu ra? COA=AOY mà COA - AOY=45°( what?) Rồi C mày lấy ở đâu? Làm như lồn ấy.


Bạn có thể vẽ ra tập rồi trả lời câu hỏi mới dễ bạn à.
Còn trên đây mk ko biết vẽ hình.
Hoặc bạn có thể vào học 24 hoặc câu hỏi tương tự tham khảo.
Chúc bạn học tốt !

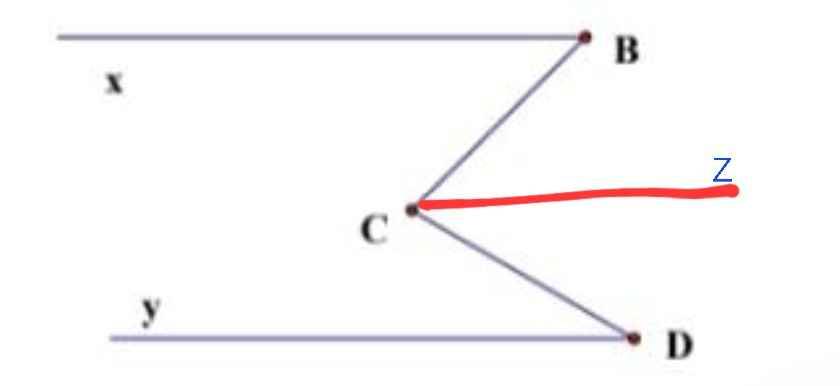
Vẽ tia Cz // Bx // Cy
Do Bx // Cz
⇒ ∠BCz = ∠xBC = 45⁰ (so le trong)
Do Cz // Dy
⇒ ∠DCz = ∠CDy = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCz + ∠DCz
= 45⁰ + 30⁰
= 75⁰

Lời giải:
Kẻ $Dt\parallel Ex\parallel Gy$ ($Dt$ nằm cùng phía với $Ex$ trên mặt phẳng bờ $DE$)
Vì $Dt\parallel Ex$ nên:
$\widehat{xED}+\widehat{EDt}=180^0$ (2 góc trong cùng phía)
$\Rightarrow \widehat{EDt}=180^0-\widehat{xED}=180^0-120^0=60^0$
Vì $Dt\parallel Gy$ nên $\widehat{tDG}=\widehat{DGy}=30^0$ (2 góc so le trong)
$\Rightarrow \widehat{EDG}=\widehat{EDt}+\widehat{tDG}=60^0+30^0=90^0$
Bạn xem lại đề bài giúp mk nha
mình xem kĩ rồi , đề bài sai nha