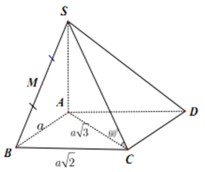
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2 , AB = a ; BC = 2a. Gọi M là trung điểm của DC. Hai mặt phẳng (SBD) và (SAM) cùng vuông góc với đáy. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Theo bài ra ta có:
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
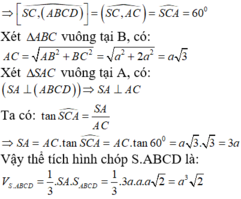

Đáp án D
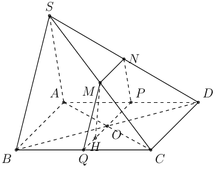
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .

Chọn D.
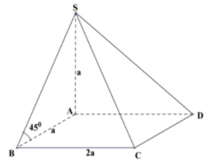
Theo giả thiết góc giữa SC và đáy bằng 60 o suy ra S C A ^ = 60 o
ABCD là hình chữ nhật nên A C = A B 2 + B C 2 = a 3
Tam giác SAC vuông tại A nên S A = A C . tan 60 o = 3 a
Diện tích đáy là S A B C D = A B . A D = 2 a 2
Thể tích khối chóp S.ABCD là V = 1 3 2 a 2 . 3 a = 2 a 3

Đáp án A
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
Xét ΔABC vuông tại B, có


Chọn đáp án D
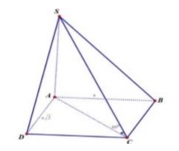
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó OI ⊥ (ABCD)
⇒ IA = IB = IC = ID với ∆ S A C vuông tại A, IA = IS = IC. Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra IA = a 2 ⇒ SC = 2a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng (ABCD).
![]()
Suy ra ∆ S A C vuông cân
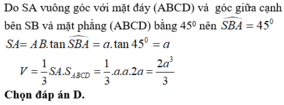
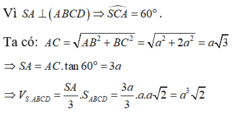

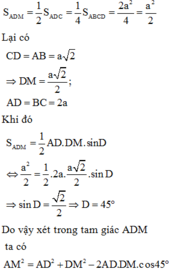
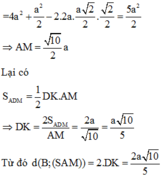
Phương pháp:
Xác định chiều cao hình chóp bằng kiến thức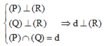
Xác định khoảng cách
Tính toán bằng cách sử dụng quan hệ diện tích, định lý hàm số cosin, công thức tính diện tích tam giác S = 1 2 a.h với a là cạnh đáy, h là chiều cao tương ứng và
Cách giải:
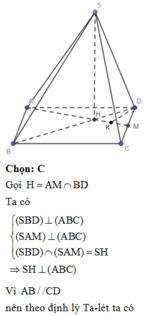
Gọi H = AM ∪ BD
Ta có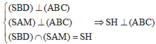
Vì AB//CD nên theo định lý Ta-lét ta có
Ta có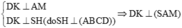
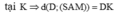
Vì M là trung điểm của DC và ABCD là hình bình hành có diện tích 2 a 2 nên ta có:
Lại có CD = AB = a 2
Khi đó

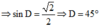
Lại có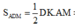
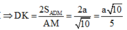
Từ đó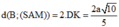
Chọn: C