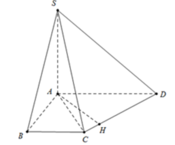
Cho hình chóp SABCD có đáy là hình thang vuông tại A;B với BC là đáy nhỏ. Biết rằng tam giác SAB đều có cạnh là 2a và nằm trong mặt phẳng vuông góc với đáy, và khoảng cách từ D tới mặt phẳng (SHC) là (H là trung điểm của AB). Thể tích khối chóp S.ABCDlà:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
H H 1 = a 2 , S H = a 3 ⇒ 1 H H 2 = 1 H H 1 2 + 1 S H 2 = 1 3 a 2 + 1 2 a 2 = 5 6 a ⇒ H H 2 = 6 5 a
⇒ d A , S C D = 30 10 a
Chọn phương án B.

Ta có: \(S_{ABCD}=\dfrac{\left(BC+AD\right).AB}{2}=\dfrac{3}{2}a^2\)
a, \(h=SA=AB.tan60^o=a\sqrt{3}\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.a\sqrt{3}=\dfrac{\sqrt{3}}{2}a^3\)
b, \(h=SA=AD.tan45^o=2a\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.2a=a^3\)
c, Dễ chứng minh được SC vuông góc với CD tại C \(\Rightarrow\widehat{SCA}=30^o\)
\(\Rightarrow h=SA=AC.tan30^o=AD.sin45^o.tan30^o=\dfrac{\sqrt{6}}{3}a\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{6}}{6}a^3\)

Ta có: \(\left\{{}\begin{matrix}AB\perp AD\left(gt\right)\\AB\perp SI\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
Mà \(AB\in\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(SAD\right)\)

Vì SA vuông góc (ABCD)
=>SA vuông góc CD
Gọi I là trung điểm của AD
=>AI=BC=a
mà AI//BC
nên AB=CI=a
=>AB=CI=ID
=>ΔACD vuông tại C
=>CD vuông góc AC
=>CD vuông góc (SAC)
=>(SCD) vuông góc (SAC)
Vẽ AE vuông góc SC tạiE
=>AE vuông góc (SCD)
mà \(A\in\left(P\right)\perp\left(SCD\right)\)
nên \(AE\in\left(P\right)\)
=>\(E=SC\cap\left(P\right)\)
\(E\in\left(P\right)\cap\left(SCI\right)\)
\(\left(P\right)\supset AB\)//CI thuộc (SCI)
=>(P) cắt (SCI)=Ex//AB//CI
Gọi F=Ex giao SI
=>(P) cắt (SAD) tại AJ
Gọi F=AJ giao SD
=>F=(P)giao (SD)
=>Tứ giác cần tìm là ABEF

Đáp án D
Dựng A H ⊥ C D suy ra AH là đường vuông góc cung của SA vad CD Ta có:
S A C D = 1 2 A D . d C ; A D = 1 2 .3 a . A B = 3 a 2 2 .
Lại có:
C D = A B 2 + A D − B C 2 = a 5 ⇒ A H = 2 S A C D C D = 3 a 5

Đáp án là C
ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊥ A B ⇒ S H ⊥ A B C D
mà D I ⊥ C H D I ⊥ S H ⇒ D I ⊥ S H C ⇒ d D , S H C = D I = 2 a 2
ta có
Δ B H C = Δ A H E ⇒ S Δ B H C = S Δ A H E ; H E = H C
mà
S A B C D = S A H C D + S Δ B H C = S A H C D + S Δ A H E = S Δ D C E
Tam giác SAB đều nên . S H = a 3
Tam giác SHC có
H C = S C 2 − S H 2 = a 2 ⇒ E C = 2 H C = 2 a 2 .
Khi đó S A B C D = S Δ D C E = 1 2 D I . E C = 4 a 2 .
Vậy V A B C D = 1 3 S H . S A B C D = 1 3 a 3 .4 a 2 = 4 a 3 3 3 .