Từ hình vẽ trên, biết \(\widehat{ACB}\)>\(\widehat{xAB}\); Ax//By. Chứng minh rằng \(\widehat{ABC}\)=\(\widehat{xAC}\)+\(\widehat{CBy}\)cAxBy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MC
25 tháng 10 2018
Bạn xem có phải hình vẽ thế này ko nhá!
A B C x M N 2 1
a, \(\widehat{NAC}=\widehat{ACB}\Rightarrow\)AN//BC (2 góc so le trong bằng nhau)
\(\Rightarrow\widehat{MAB}=\widehat{ABC}\) (2 góc so le trong)
b, Do NA//BC suy ra NM//BC suy ra
\(\widehat{MAx}=\widehat{ACB}=55^o\) (2 góc đồng vị)
c, DO \(\widehat{MAx}=\widehat{ACB}\) và \(\widehat{MAB}=\widehat{ABC}\)(chứng minh trên)
Mặt khác \(\widehat{ABC}=\widehat{ACB}\left(\widehat{B}=\widehat{C}\right)\)(giả thiết)
suy ra \(\widehat{MAx}=\widehat{MAB}\)suy ra MA là tia phân giác của \(\widehat{BAx}\)
18 tháng 9 2023
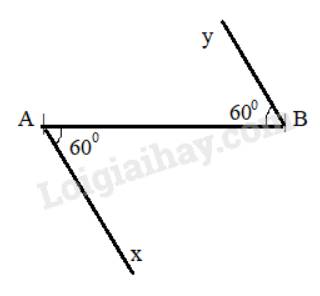
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
MC
7 tháng 10 2018
\(\angle xAB=\dfrac{7}{2} \angle ABy\)
nếu bạn vẽ góc ABy = 30 độ thì vẽ góc xAB=105 độ
A B x y
hình đâu bạn
cAxBy