cho hình vẽ biết AB=DB;AC=DC
a)chứng minh góc BAC=BDC
b) BC là phân giác của ABD A B D C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 3 2022
\(DE=EC\\ \Rightarrow DE//BC\\ \Rightarrow\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{6}=\dfrac{6}{x}\\ \Rightarrow x=9\)
CM
7 tháng 3 2018
Qua I và C vẽ các đường thẳng IP và CQ vuông góc với BD, IH vuông góc với DC.
CM
27 tháng 9 2017
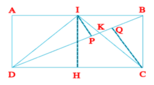
Qua I và C vẽ các đường thẳng IP và CQ vuông góc với BD, IH vuông góc với DC.
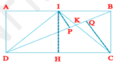
Ta có S A D B = S C D B = 1 2 S A B C D và S D I B = 1 2 S A D B (vì có chung đường cao DA, IB = 1/2 AB),
S D I B = 1 2 S D B C . Mà 2 tam giác này có chung đáy DB
Nên IP = 1/2 CQ. S I D K = 1 2 S C D K (vì có chung đáy DK và IP = 1/2 CQ)
S C D I = S I D K + S D K C = 3 S D I K .
Ta có :
S A D I = 1 2 AD x AI, S D I C = 1 2 IH x DC
Mà IH = AD, AI = 1/2 DC, S D I C = 2 S A D I n ê n S A D I = 3 2 S D I K
Vì AIKD là phần được tô màu vàng nên S A I K D = 20 ( c m 2 )
S D A I + S I D K = 20 ( c m 2 )
S D A I + 2 3 S A D I = 20 ( c m 2 )
S D A I = (3 x 20)/5 = 12 ( c m 2 ) ;
Mặt khác S D A I = 1 2 S D A B = 1 4 S A B C D
1 tháng 8 2023
a: Sửa đề; DH=16cm
DC=16+9=25cm
DB=căn DH^2+HB^2=20cm
BC=căn 12^2+9^2=15cm
b: Xét ΔDBC có
DC^2=DB^2+BC^2
nên ΔBDC vuông tại B
c: ΔBDC vuông tại B có sin C=BD/DC=4/5
nên \(\widehat{C}\simeq53^0\)
=>\(\widehat{B}\simeq180^0-53^0=127^0\)
Kẻ AK vuông góc DC
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AK=BH=12cm
Xét ΔAKD vuông tại K có sin D=AK/AD=6/7
nên \(\widehat{D}\simeq59^0\)
=>góc A=180 độ-59 độ=121 độ
1 tháng 8 2023
a: Sửa đề; DH=16cm
DC=16+9=25cm
DB=căn DH^2+HB^2=20cm
BC=căn 12^2+9^2=15cm
b: Xét ΔDBC có
DC^2=DB^2+BC^2 nên ΔBDC vuông tại B
c: ΔBDC vuông tại B có sin C=BD/DC=4/5 nên ˆ C ≃ 53*(*là độ C)
=> ˆ B ≃ 180* − 53* = 127*
Kẻ AK vuông góc DC
Xét tứ giác ABHK có: AB//HK AK//HB
=>ABHK là hình bình hành
=>AK=BH=12cm Xét ΔAKD vuông tại K có sin D=AK/AD=6/7 nên ˆ D ≃ 59*
=>góc A=180 độ-59 độ=121 độ
15 tháng 6 2023
b: Xét tứ giác AEPF có
AE//PF
AF//PE
góc FAE=90 độ
=>AEPF là hcn
=>góc AEF=góc APF=góc ADB
=>FE//BD
PT
1
CM
10 tháng 1 2019
Vì DE // BC, theo định lý Ta-lét ta có
A D D B = A E E C ⇔ A D 18 = 12 36 − 12 ⇔ A D 18 = 12 24
=> AD = 18.12 24 = 9 cm
Nên AB = AD + DB = 9 + 18 = 27 cm
Đáp án: D
5 tháng 1 2022
a: Xét tứ giác MBNC có
MB//NC
NB//MC
Do đó: MBNC là hình bình hành
mà \(\widehat{BMC}=90^0\)
nên MBNC là hình chữ nhật
b: Ta có: MBNC là hình chữ nhật
nên MN=BC
mà BC=AB
nên MN=AB