Cho hình bình hành ABCD (góc A > 900 ; AB > BC). Qua C dựng đường thẳng vuông góc BC, trên đó lấy M, N sao cho CM = CN = CB. Qua C dựng đường thẳng vuông góc với CD, trên đó lấy điểm P, Q sao cho CP = CQ = CD. (M và P nằm cùng phía đối với BC)
Chứng minh rằng AC vuông góc với MP.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) AD = DM ( gt )
⇒ ∆ ADM cân
⇒ \(\widehat{DAM}=\widehat{AMD}\)
mà \(\widehat{DAM}=\widehat{AMD}\) ( 2 góc so le trong )
⇒ \(\widehat{DAM}=\widehat{BAM}\)
⇒ AM la tia phân giác \(\widehat{A}\)
Do AD = BC (ABCD là hình bình hành)
⇒ BC = MC
⇒ △ CMB cân
⇒ \(\widehat{CMB}=\widehat{CBM}\)
mà \(\widehat{ABM}=\widehat{CMB}\) (2 góc so le trong do AB // MC)
⇒ \(\widehat{ABM}=\widehat{CBM}\)
⇒ BM là tia phân giác của \(\widehat{B}\)
b) Lấy E là trung điểm của AB
ta có AE = DM ( do AB = DC)
mà AE // DM ( do AB // CD )
⇒ Tứ giác AEDM là hình bình hành
⇒ AD = EM
mà AD =\(\dfrac{1}{2}\) AB
⇒ EM = \(\dfrac{1}{2}\) AB
⇒ ∆ AMB vuông tại M (vì trong tam giác có đường trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông)
⇒ \(\widehat{AMB}=90^0\) ( đpcm )
1: Ta có: AB=2AD
mà AB=CD
nên CD=2AD
mà \(CD=2\cdot MD\cdot MC\)
nên AD=DM=MC=BC
Xét ΔAMD có DA=DM
nên ΔAMD cân tại D
Suy ra: \(\widehat{DAM}=\widehat{DMA}\)
mà \(\widehat{DMA}=\widehat{MAB}\)
nên \(\widehat{DAM}=\widehat{BAM}\)
hay AM là tia phân giác của \(\widehat{DAB}\)
Xét ΔBCM có MC=MB
nên ΔBMC cân tại C
Suy ra: \(\widehat{CMB}=\widehat{CBM}\)
mà \(\widehat{CMB}=\widehat{ABM}\)
nên \(\widehat{CBM}=\widehat{ABM}\)
hay BM là tia phân giác của \(\widehat{ABC}\)

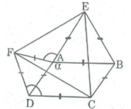
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.

Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ

a) ABCD là hình bình hành => AD=BC, AD//BC
--->Dễ dàng có được \(\Delta AED=\Delta CFB\left(c.g.c\right)\Rightarrow AE=CF\)
Mà AE//CF (cùng vuông góc BD) => AECF là hình bình hành.
b) AHDK không thể là hình bình hành nha --> phải là AHCK
Chứng minh: AH//CK (cùng vuông góc BD)
CH//AK (vì ABCD là hình bình hành)
=> AHCK là hình bình hành