Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD; AB>CD). Gọi M, N lần lượt là trung điểm các cạnh SA, SB.
a) Chứng minh: MN//CD.
b) Tìm P = SC \(\cap\) (ADN).
c) Kéo dài AN và DP cắt nhau ở I. Chứng minh: SI//AB//CD. Tứ giác SABI là hình gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 2 2019
Đáp án A
ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
22 tháng 9 2023
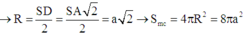
Tham khảo:
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng các mặt bên là hình tam giác
Hình thang ABCD có AB//CD và AB=2cm, CD=6cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba đáy BC
Từ đó, ta vẽ được hình biểu diễn của S.ABCD.
CM
26 tháng 7 2019
Đáp án A
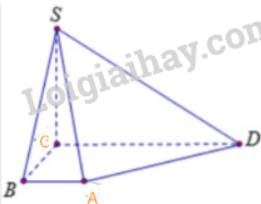
Do M N / / A D nên giao tuyến của (SAD) và (GMN) song song với AD
Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P
Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do đó thiết diện là hình bình hành
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2022
IJ là đường trung bình của hình thang \(\Rightarrow\left\{{}\begin{matrix}IJ||AB\\IJ=\dfrac{AB+CD}{2}\end{matrix}\right.\)
Qua G kẻ đường thẳng song song AB lần lượt cắt SB, SA tại E và F
\(\Rightarrow\) Tứ giác IJEF là thiết diện của (GIJ) và chóp
\(EF||AB||IJ\Rightarrow IJEF\) là hình thang
Gọi M là trung điểm AB
Theo tính chất trọng tâm và định lý Talet:
\(\dfrac{EF}{AB}=\dfrac{SG}{SM}=\dfrac{2}{3}\)
Để IJEF là hình bình hành \(\Leftrightarrow IJ=EF\)
\(\Leftrightarrow\dfrac{2}{3}AB=\dfrac{AB+CD}{2}\Leftrightarrow\dfrac{1}{3}AB=CD\)
\(\Rightarrow AB=3CD\)
CM
23 tháng 11 2017
Đáp án A
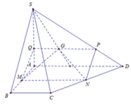
Do M N / / A D nên giao tuyến của S A D và G M N song song với AD. Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P. Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do thiết diện là hình bình hành
CM
2 tháng 5 2017
Đáp án A
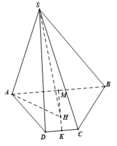
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) 
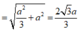
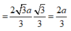
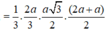
a/ MN//AB (t/c đường trung bình)
Mà AB//CD \(\Rightarrow\) MN//CD
b/ Kéo dài AD cắt BC tại E
Nối NE cắt SC tại P \(\Rightarrow P=SC\cap\left(ADN\right)\)
c/ Ta có SI là giao tuyến của (SAB) và (SCD)
Ba mặt phẳng (SAB); (SCD); (ABCD) cắt nhau theo 3 giao tuyến phân biệt là SI; AB; CD.
Mà AB//CD \(\Rightarrow\) SI//AB//CD