Có bao nhiêu giá trị nguyên thuộc đoạn của tham số m để đồ thị hàm số có đúng bốn đường tiệm cận?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A

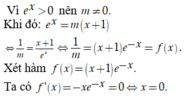

Dựa vào BBT, ta thấy phương trình có nghiệm duy nhất
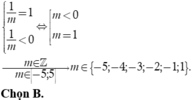
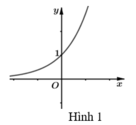
Ta có y = e x là hàm đồng biến trên ℝ và y = e x > 0 với mọi x ∈ ℝ có đồ thị (C)(xem hình 1).
Do đó:
= Nếu m < 0 thì y = m(x+1) là hàm số nghịch biến trên ℝ , có đồ thị là một đường thẳng luôn qua điểm (-1;0) nên luôn cắt đồ thị (C): y = e x tại duy nhất một điểm.
= Nếu m = 0 phương trình vô nghiệm (do y = e x > 0).
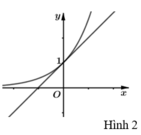
= Nếu m > 0 để phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng
![]() là tiếp tuyến của (C) (như hình 2)
là tiếp tuyến của (C) (như hình 2)
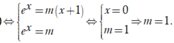


+) Phương trình ban đầu có nghiệm khi và chỉ khi phương trình bậc hai ẩn t có nghiệm dương.
Cách giải:

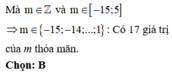


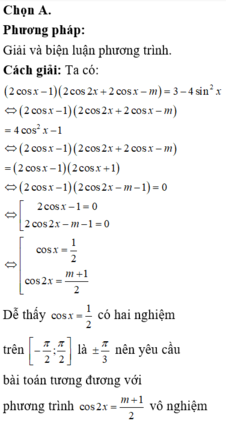

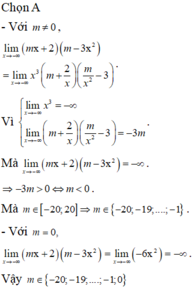




Chọn đáp án C