Tính khoảng cách từ A(2;5) đến đường thẳng (∆):{x=5-t và y=-2+t
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
OY
22 tháng 12 2021
Câu 16: Khoảng cách từ ảnh của vật đến gương phẳng có tính chất nào sau đây?
A. Bằng khoảng cách từ vật đến gương
B. Nhỏ hơn khoảng cách vật đến gương
C. Lớn gấp 2 lần khoảng cách từ vật đến gương
D. Lớn gấp 4 lần khoảng cách từ vật đến gương
Câu 17: Ảnh của vật tạo bởi gương cầu lồi có tính chất nào sau đây?
A. Ngược chiều so với vật B. Cùng chiều so với vật
C. Gương to thì ảnh cùng chiều với vật D. Gương nhỏ thì ảnh ngược chiều với vật
Câu 18: Ảnh của vật tạo bởi gương cầu lõm có tính chất nào sau đây?
A. Ngược chiều so với vật B. Cùng chiều so với vật
C. Gương to thì ảnh cùng chiều với vật D. Gương nhỏ thì ảnh ngược chiều với vật
Câu 19: Ảnh ảo của vật tạo bởi gương cầu lõm luôn?
A. Lớn bằng vật B. Nhỏ hơn vật C. Lớn hơn vật
Câu 20: Âm thanh được tạo ra nhờ:
A. Nhiệt B. Điện C. Ánh sáng D. Dao động
Câu 21: Số dao động trong một giây gọi là?
A. Độ dài B. Tần số C. Khối lượng D. Trọng lượng
TP
11 tháng 7 2016
Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà
21 tháng 6 2016
ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
21 tháng 6 2016
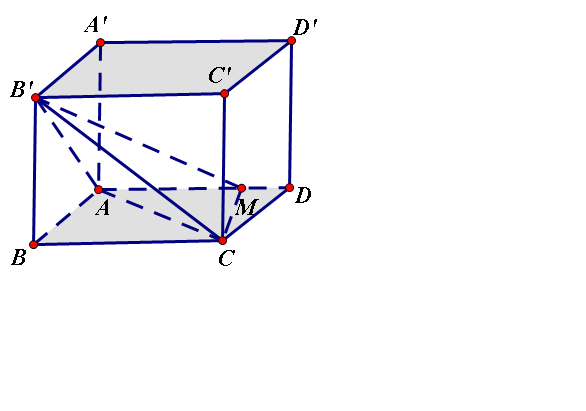
Pytago tính đuợc 3 cạnh ΔAMC
\(AC=a\sqrt{5}\); \(AM=\frac{3a}{2}\), \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức HeronHeron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức HeronHeron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)
20 tháng 9 2021
\(a,\) Pt hoành độ giao điểm
\(x=0\\ \Leftrightarrow y=-2\cdot0+3=3\\ \Leftrightarrow A\left(0;3\right)\)
Pt tung độ giao điểm
\(y=0\\ \Leftrightarrow0=-2x+3\Leftrightarrow x=\dfrac{3}{2}\\ \Leftrightarrow B\left(\dfrac{3}{2};0\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\) \(\Rightarrow SH\perp CD\)
Gọi E là trung điểm CD \(\Rightarrow HE||BC\Rightarrow HE\perp CD\)
\(\Rightarrow CD\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a), \(HE=BC=a\)
Hệ thức lượng: \(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Do \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=\dfrac{a\sqrt{21}}{7}\)
b.
Theo tính chất trọng tâm, ta có \(GS=\dfrac{2}{3}HS\)
Mà \(HG\cap\left(SCD\right)=S\Rightarrow d\left(G;\left(SCD\right)\right)=\dfrac{2}{3}d\left(H;\left(SCD\right)\right)=\dfrac{2a\sqrt{21}}{21}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
c.
Từ H kẻ \(HK\perp SA\)
Do \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HK\)
\(\Rightarrow HK\perp\left(SAD\right)\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(HK=\dfrac{SH.AH}{\sqrt{SH^2+AH^2}}=\dfrac{a\sqrt{3}}{4}\)
Do \(BC||AD\Rightarrow BC||\left(SAD\right)\Rightarrow d\left(BC;SD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà \(\left\{{}\begin{matrix}BH\cap\left(SAD\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(BC;SD\right)=d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)=\dfrac{a\sqrt{3}}{2}\)
câu hỏi từ 4 năm trước của e nó vẫn ko ai trả lời =(