Bài 1: Cho 2 điểm A(1;2), B(3;4).
a) Viết phương trình đường thẳng AB.
b) Tìm trên trục tung 1 điểm M để 3 điểm A,M,B thẳng hàng.
Bài 2: Cho HPT: (II) \(\left\{{}\begin{matrix}x-y=2\\mx-y=3\end{matrix}\right.\)
Định m để HPT (II) có nghiệm duy nhất thuộc góc phần tư thứ I của mp tọa độ

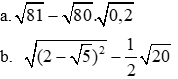
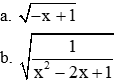
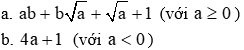
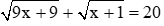
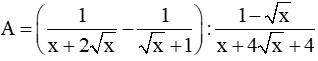
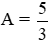
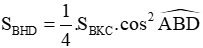
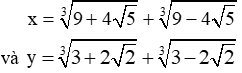

 với x ³ 0 và x ¹ 1.
với x ³ 0 và x ¹ 1.

 với x > 2017
với x > 2017
Bài 1 :
a, - Gọi phương trình đường thẳng AB là \(y=ax+b\)
- Thay \(x=1,y=2\) vào phương trình trên ta được :
\(a+b=2\) ( I )
- Thay \(x=3,y=4\) vào phương trình trên ta được :
\(3a+b=4\left(II\right)\)
- Từ ( I ) và ( II ) ta có hệ phương trình : \(\left\{{}\begin{matrix}a+b=2\\3a+b=4\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a=2-b\\3\left(2-b\right)+b=4\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a=2-b\\6-3b+b=4\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a=2-b\\-2b=-2\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a=2-1=1\\b=1\end{matrix}\right.\)
- Thay \(a=1,b=1\) vào phương trình ( I ) ta được :
\(y=x+1\)
b, - Gỉa sử tọa độ của điểm M là \(\left(x_1;y_1\right)\)
Mà điểm M nằm trên trục tung nên hoành độ của nó bằng 0 .
=> Tọa độ của điểm M là : \(\left(0;y_1\right)\)
Ta có : \(\overrightarrow{AB}\left(1;1\right)\) và \(\overrightarrow{AM}\left(0-1;y_1-2\right)\)
- Để 3 điểm A; B; M thẳng hàng thì \(\overrightarrow{AB}\) cùng phương với \(\overrightarrow{AM}\)
=> \(\frac{1}{-1}=\frac{1}{y_1-2}\)
=> \(y_1-2=-1\)
=> \(y_1=1\)
Vậy tọa độ của điểm M \(\left(0;1\right)\)
- Để hệ phương trình có nghiệm duy nhất thì :
\(\frac{1}{m}\ne\frac{-1}{-1}\ne1\left(m\ne0\right)\)
=> \(m\ne1\)
- Ta có hệ phương trình : \(\left\{{}\begin{matrix}x-y=2\\mx-y=3\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=2+y\\m\left(2+y\right)-y=3\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=2+y\\2m+my-y=3\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=2+\frac{3-2m}{m-1}=\frac{2\left(m-1\right)+\left(3-2m\right)}{m-1}=\frac{2m-2+3-2m}{m-1}=\frac{1}{m-1}\\y=\frac{3-2m}{m-1}\end{matrix}\right.\)
- Để hệ phương trình thuộc góc phần tư thứ nhất thì :
\(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\) ( I )
- Thay \(x=\frac{1}{m-1};y=\frac{3-2m}{m-1}\) vào ( I ) ta được :
\(\left\{{}\begin{matrix}\frac{1}{m-1}>0\\\frac{3-2m}{m-1}>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}m-1>0\\3-2m>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}m-1>0\\3-2m>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}m>1\\m< \frac{3}{2}\end{matrix}\right.\)
=> \(1< m< \frac{3}{2}\)
Vậy để hệ phương trình trên thuộc góc phần tư số 1 thì \(1< m< \frac{3}{2}\)