tìm m để hệ phương trình mx-y=2;3x+my=1-2m có nghiệm (x,y) thoả mãn x-3y=6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SA
24 tháng 2 2021
a) Với m = -2
=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Vậy S = {0; 2}
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\)
=> x + mx = 2 + m
<=> x(m + 1) = 2 + m
Để hpt có nghiệm duy nhất <=> \(m\ne-1\)
<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)
=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)
Mà 3x - y = -10
=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)
<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)
<=> 6m = -8
<=> m = -4/3
c) Để hpt có nghiệm <=> m \(\ne\)-1
Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)
Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)
Để x nguyên <=> 1 \(⋮\)m + 1
<=> m +1 \(\in\)Ư(1) = {1; -1}
<=> m \(\in\) {0; -2}
Thay vào y :
với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)
m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)
Vậy ....
T
18 tháng 1 2021
Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
CM
18 tháng 4 2018
Đáp án C
Nghiệm phương trình y = (-2 - m)x + 2 được biểu diễn bởi đường thẳng (d1): y =(-2 - m)x + 2
Nghiệm phương trình y = (m + 4)x + 19 được biểu diễn bởi đường thẳng (d2): y = (m +4)x +19
Để hệ phương trình đã cho có nghiệm duy nhất khi và chỉ khi hai đường thẳng cắt nhau nên:
-2 - m ≠ m + 4 ⇔ -2m ≠ 6 ⇔ m ≠ -3
12 tháng 1 2023
a: Khi m=-2 thì hệ sẽ là:
y+4=5 và -2x+3y=1
=>y=1 và -2x=1-3y=1-3=-2
=>x=1 và y=1
b: \(\left\{{}\begin{matrix}y=2m+5\\mx+3\left(2m+5\right)=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2m+5\\mx=1-6m-15=-6m+14\end{matrix}\right.\)
=>x=-6m+14/m và y=2m+5
Để hệ có nghiệm (x,y)>0 thì -6m+14/m>0 và 2m+5>0
=>m>-5/2 và \(\dfrac{6m-14}{m}< 0\)
=>m>-5/2 và 0<m<7/3
=>0<m<7/3
NM
Nguyễn Minh Quang
Giáo viên
19 tháng 1 2021
a, tại m=2 thì hệ tương đương với\(\hept{\begin{cases}x+2y=2\\2x-y=2\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=2\\4x-2y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x+2y=2\\5x=6\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{6}{5}\\y=\frac{2}{5}\end{cases}}}} }\)
b, do thay (x,y)=(2,-1) vào phương trình x+2y=2 không thỏa mãn nên hệ phương trình không nhận cặp (x,y)=(2,-1) là nghiệm
Y
26 tháng 4 2022
Thay \(m=-2\) vào \(mx-y=m\) \(\Leftrightarrow-2x-y=-2\)
\(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y=-4\\-2x-y=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y+2x+y=-4-\left(-2\right)\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=-2\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x+2=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=0\end{matrix}\right.\)
Vậy tập nghiệm có hệ pt : \(\left(x;y\right)=\left(0;2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
a.
Với \(m=-2\Rightarrow\left\{{}\begin{matrix}x+y=2\\-2x+y=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\3x=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=2-\dfrac{4}{3}=\dfrac{2}{3}\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}x+y=2\\mx+y=m\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\\left(m-1\right)x=m-2\end{matrix}\right.\)
Phương trình có nghiệm khi \(m\ne1\)
Khi đó: \(x=\dfrac{m-2}{m-1}=1-\dfrac{1}{m-1}\)
\(x\in Z\Rightarrow\dfrac{1}{m-1}\in Z\Rightarrow m-1=Ư\left(1\right)=\left\{-1;1\right\}\)
\(\Rightarrow m=\left\{0;2\right\}\)
14 tháng 5 2021
`x-y=2<=>x=y+2` thay vào trên
`=>m(y+2)+2y=m+1`
`<=>y(m+2)=m+1-2m`
`<=>y(m+2)=1-2m`
Để hpt có nghiệm duy nhất
`=>m+2 ne 0<=>m ne -2`
`=>y=(1-2m)/(m+2)`
`=>x=y+2=5/(m+2)`
`xy=x+y+2`
`<=>(5-10m)/(m+2)=(6-2m)/(m+2)+2`
`<=>(5-10m)/(m+2)=10/(m+2)`
`<=>5-10m=10`
`<=>10m=-5`
`<=>m=-1/2(tm)`
Vậy `m=-1/2` thì HPT có nghiệm duy nhât `xy=x+y+2`
14 tháng 5 2021
`a)m=2`
$\begin{cases}2x+2y=3\\x-y=2\end{cases}$
`<=>` $\begin{cases}2x+2y=3\\2x-2y=4\end{cases}$
`<=>` $\begin{cases}4y=-1\\x=y+2\end{cases}$
`<=>` $\begin{cases}y=-\dfrac14\\y=\dfrac74\end{cases}$
Vậy m=2 thì `(x,y)=(7/4,-1/4)`
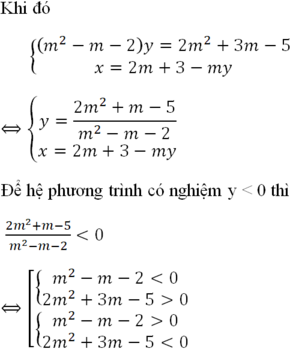
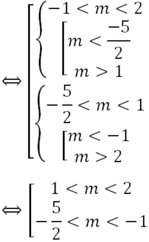
Để hệ có nghiệm duy nhất thì \(\frac{m}{3}<>-\frac{1}{m}\)
=>\(m^2<>-3\) (luôn đúng)
\(\begin{cases}mx-y=2\\ 3x+my=1-2m\end{cases}\Rightarrow\begin{cases}y=mx-2\\ 3x+m\left(mx-2\right)=1-2m\end{cases}\)
=>\(\begin{cases}y=mx-2\\ 3x+m^2x-2m=1-2m\end{cases}\Rightarrow\begin{cases}y=mx-2\\ x\left(m^2+3\right)=1\end{cases}\)
=>\(\begin{cases}x=\frac{1}{m^2+3}\\ y=mx-2=\frac{m}{m^2+3}-2=\frac{m-2m^2-6}{m^2+3}=\frac{-2m^2+m-6}{m^2+3}\end{cases}\)
x-3y=6
=>\(\frac{1}{m^2+3}-3\cdot\frac{-2m^2+m-6}{m^2+3}=6\)
=>\(\frac{1+6m^2-3m+18}{m^2+3}=6\)
=>\(6m^2-3m+19=6\left(m^2+3\right)=6m^2+18\)
=>-3m=-1
=>\(m=\frac13\) (nhận)