1)a)Khi nào số a là nghiệm của P(x)
b)Số nào là nghiệm của đa thức x^2-2x^3
Số -1;0;1;2;3
câu 2) cho M(x)=(4x^2+2x^3-x^2+2x^4)-(x^4+3x^2+x-5)
a) Thu gọn và sắp xép đa thức theo lũy thừa giảm dần của biến
b)Tính M(1),M(-1/2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thu
16 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
11 tháng 5 2021
Ta có : \(A\left(x\right)=2x+6\)
Vì x = -3 là nghiệm của đa thức trên nên thay x = -3 vào đa thức trên ta được :
\(-6+6=0\)* đúng *
Vậy x = -3 là nghiệm đa thức trên
CM
3 tháng 7 2017
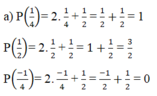
Vậy x =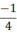 
là nghiệm của đa thức P(x) = 2x +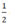 
b) Q(3) = 32 – 2.3 – 3 = 9 – 6 – 3 = 0
Q(1) = 12 – 2.1 – 3 = 1 – 2 – 3 = - 4
Q(-1) = (-1)2 – 2.(-1) – 3 = 1 + 2 – 3 = 0
Vậy x = 3 và x = - 1 là nghiệm của đa thức Q(x) = x2 – 2x – 3
10 tháng 4 2016
a. Khi thay x = a mà P(x) = 0 thì a được gọi là nghiệm của đa thức P(x)
b. Có P(x) = 6 + 2x = 0
2x = 0 - 6
2x = -6
x = -6 : 2
x = -3
DN
5 tháng 3 2023
\(R\left(x\right)=x^2+3x\)
a) Ta có:
\(R\left(x\right)=x^2+3x\)
\(R\left(x\right)=x\left(x+3\right)\)
\(R\left(x\right)=x\left(x+3\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x+3=0\Rightarrow x=-3\end{matrix}\right.\)
Vậy: Trong các số -1, -2 và -3 thì nghiệm của đa thức là -3
b) Các nghiệm của R(x) là 0 và -3 (ở phần a)
RA
16 tháng 4 2019
Bài 1:
a)Số a được gọi là nghiệm của đa thức P(x) khi có P(a)=0
b)Ta có P(x)=6+2x có nghiệm khi:
6+2x=0
2x=-6
x=\(\frac{-6}{2}\)=-3
23 tháng 4 2019
a, Với x=1
\(P\left(x\right)=2+1-1=2\)
Với x=\(\frac{1}{4}\)
\(P\left(x\right)=\frac{1}{8}+\frac{1}{4}-1=-\frac{5}{8}\)
23 tháng 4 2019
Thay ba số -1;1;2 vào
Các số trên k có số nào là nghiệm của dt P(x)
Hok tốt
21 tháng 5 2022
\(f\left(1\right)=1^4+2\cdot1^3-2\cdot1^2-6\cdot1+5\)
\(=1+2-2-6+5=0\)
=>x=1 là nghiệm
\(f\left(-1\right)=\left(-1\right)^4+2\cdot\left(-1\right)^3-2\cdot\left(-1\right)^2-6\cdot\left(-1\right)+5\)
\(=1-2-2+6+5=12-4=8\)
=>x=-1 không là nghiệm
\(f\left(2\right)=2^4+2\cdot2^3-2\cdot2^2-6\cdot2+5\)
\(=16+16-8-12+5=8+4+5>0\)
Do đó: x=2 không là nghiệm
\(f\left(-2\right)=\left(-2\right)^4+2\cdot\left(-2\right)^3-2\cdot\left(-2\right)^2-6\cdot\left(-2\right)+5\)
\(=16-16-2\cdot4+12+5=17-8=9>0\)
Do đó: x=-2 không là nghiệm
7 tháng 5 2023
a. Thay x = 1 vào đa thức ta có:
\(1^2-4.1+4=1\)
Thay x = 2 vào đa thức ta có
\(2^2-4.2+4=0\)
Thay x = 3 vào đa thức ta có:
\(3^2-4.3+4=1\)
Thay x = -1 vào đa thức ta có:
\(\left(-1\right)^2-4.\left(-1\right)+4=9\)
b. Trong các số trên 2 là nghiệm của đa thức M(x)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 5 2023
a, M(\(x\)) = \(x^2\) - 4\(x\) + 4
M(1) = 12 - 4.1 + 4 = 1
M(2) = 22 - 4.2 + 4 = 0
M(3) = 32 - 4.3 + 4 = 1
M(-1) = (-1)2 - 4.(-1) + 4 = 9
b, Trong các số 1; 2; 3 và -1 thì 2 là nghiệm của M(\(x\)) vì M(2) = 0