Tổng các nghiệm thuộc đoạn [0; 3π] của phương trình 1 - 2 cos^2 x - sin x = 0 là
A. 5/3π. B. 4π. C. 6π. D. 7/2π .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có sin 2 2 x + 3 sin 2 x + 2 = 0 ⇔ sin 2 x + 1 sin 2 x + 2 = 0 ⇔ sin 2 x = - 1 ⇔ 2 x = - π 2 + k 2 π ⇔ x = - π 4 + k π mà x ∈ 0 ; 10 π suy ra 0 ≤ - π 4 + k π ≤ 10 π ⇔ 1 4 ≤ k ≤ 41 4 → k ∈ ℤ k = 1 ; 2 ; . . . ; 10
Vậy tổng tất cả các nghiệm của phương trình là T = 10 . - π 4 + 1 + 2 + . . . + 10 π = 105 2 π .

\(cos^4x-sin^4x=sin3x+cos4x\)
\(\Leftrightarrow\left(cos^2x+sin^2x\right)\left(cos^2x-sin^2x\right)=sin3x+cos4x\)
\(\Leftrightarrow cos2x=sin3x+cos4x\)
\(\Leftrightarrow cos4x-cos2x+sin3x=0\)
\(\Leftrightarrow-2sin3x.sinx+sin3x=0\)
\(\Leftrightarrow sin3x\left(1-2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin3x=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{3}\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{0;\dfrac{\pi}{3};\dfrac{2\pi}{3};\pi;\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}\)
\(\Rightarrow\sum x=3\pi\)

Đáp án A
Ta có sin 2 x + 9 π 2 = sin 2 x + π 2 + 4 π = cos 2 x và cos x − 15 π 2 = − sin x
Khi đó, phương trình (I) ⇔ cos 2 x + 3 sin x = 1 + 2 sin x ⇔ 1 − 2 sin 2 x = 1 − sin x ⇔ sin x = 0 sin x = 1 2
Kết hợp với x ∈ 0 ; 2 π , ta được x = 0 ; π ; 2 π ; π 6 ; 5 π 6 là các nghiệm của phương trình

\(2sinx-\sqrt{3}=0\)
\(\Leftrightarrow sinx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(0\le\dfrac{\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{6}\le k\le\dfrac{5}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{\pi}{3}\)
\(0\le\dfrac{2\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{3}\le k\le\dfrac{4}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{2\pi}{3}\)
\(\Rightarrow x_1+x_2=\pi\)
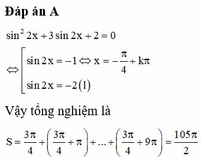
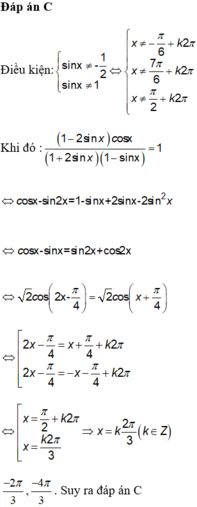
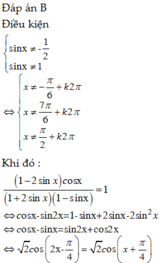
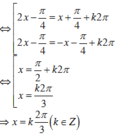
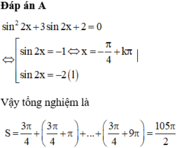
\(1-2cos^2x-sinx=0\)
\(\Leftrightarrow1-2\left(1-sin^2x\right)-sinx=0\)
\(\Leftrightarrow2sin^2x-sinx-1=0\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{2};\dfrac{7\pi}{6};\dfrac{11\pi}{6};\dfrac{5\pi}{2}\right\}\)
\(\Rightarrow\sum x=6\pi\)