Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có trực tâm H. Bt điểm B(2;7) , C(-3;-8),H(0;3) và đg trung tuyến kẻ từ điểm A nằm trên đg thg tenta : 5x-7y-1=0 Lập PTTQ của đg cao AH và tìm tọa độ điểm A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)

Câu 1: Chưa đủ dữ kiện để làm. Bạn xem lại đề.
Câu 2: Gọi tọa độ điểm H(a,b)
Ta có: \(\overrightarrow{AH}=(a-3; b-2); \overrightarrow{BC}=(1;8); \overrightarrow{BH}=(a-4; b+1); \overrightarrow{AC}=(2; 5)\)
Vì H là trực tâm tam giác ABC nên:
\(\left\{\begin{matrix} \overrightarrow{AH}.\overrightarrow{BC}=0\\ \overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a-3+8(b-2)=0\\ 2(a-4)+5(b+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+8b=19\\ 2a+5b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-71}{11}\\ b=\frac{35}{11}\end{matrix}\right.\)

Cho hình vẽ
A B C D I F
Tam giác BEC cân và có \(\widehat{BEC}=150^o\) \(\Rightarrow\) tam giác BEC cân tại E
Gọi H là hình chiếu của E lên AD \(\Rightarrow\) H là trung điểm AD và HE \(=\) d E; AD \(=\) 3
Đặt cạnh hình vuông là \(AB=x\)
Tam giác BEC cân tại E có \(\widehat{BEC}=150^o\Rightarrow\widehat{BEC}=15^o\) . Gọi I là trung điểm của \(BC\Rightarrow BI=\frac{x}{2};EI=x-3\)
Tam giác BIE vuông tại I có góc \(\widehat{EBI}=15^o\Rightarrow tan15^o=\frac{EI}{BI}=\frac{2x-6}{x}\)
\(\Rightarrow2-\sqrt{3}=\frac{2x-6}{x}\Leftrightarrow x=2\sqrt{3}\)
Phương trình đường thẳng EH qua điểm E và vuông góc với \(AD\Rightarrow EH\div4x+3y+4=0\)
Đường thằng \(AB\\ EH\Rightarrow AB\) có dạng \(''d''\div4x+3y+a=0\)
Ta có d \(''E,AB''=\frac{⊥a-4⊥}{5}=BI=\sqrt{3}\Leftrightarrow a=4⊥5\sqrt{3}\)
Phương trình đường thẳng AB là \(''d''\div4x+3y+4⊥5\sqrt{3}=0\)
P/s; Bộ khó lắm à .
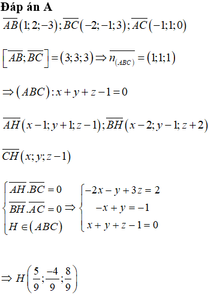
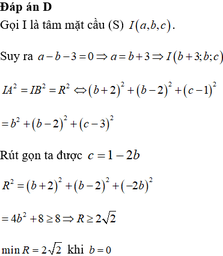

\(\overrightarrow{BC}=\left(-5;-15\right)=-5\left(1;3\right)\)
Đường thẳng AH vuông góc BC nên nhận \(\left(1;3\right)\) là 1 vtpt
Phương trình AH:
\(1\left(x-0\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-9=0\)
A là giao điểm AH và denta nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+3y-9=0\\5x-7y-1=0\end{matrix}\right.\) \(\Rightarrow A\left(3;2\right)\)