Cho tam giác ABC có đỉnh B(-1;3), trung tuyến AM có phương trình 3x+2y-9=0: trung tuyến CN: x-1=0
a) Viết pt tổng quát đường trung tuyến BE
b) Tìm tọa độ các đỉnh AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 9 2023
Tham khảo:
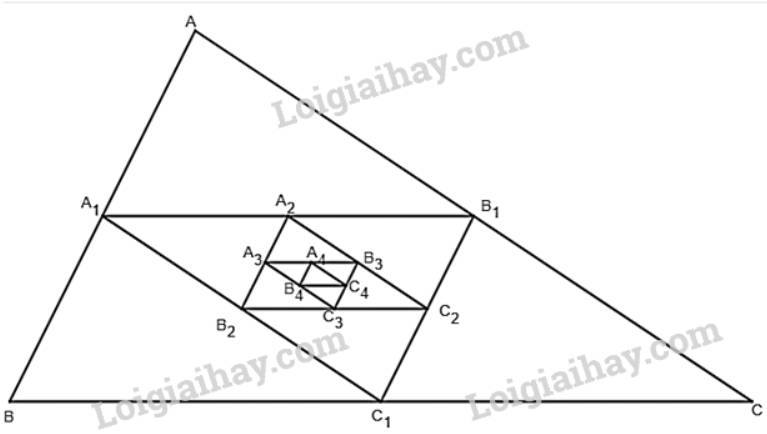
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
CM
14 tháng 11 2019
Đáp án: A
Ta có: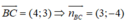 
Đường thẳng BC đi qua B và có vecto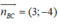 
là vecto pháp tuyến:
BC: 3(x + 1) - 4(y - 0) = 0 ⇔ 3x - 4y + 3 = 0
Gọi AH là đường cao của tam giác ABC
22 tháng 3 2017
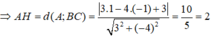
A B C M N E H
goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)
CM
9 tháng 8 2018
Đáp án: B
Ta có A(-1;3), B(1;0) và C(2;-1)
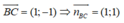
Phương trình đường thẳng BC có dạng: (x - 1) + (y - 0) = 0 ⇔ x + y - 1 = 0
Độ dài đường cao của tam giác ABC kẻ từ điểm C chính bằng khoảng cách từ điểm A đến đường thẳng BC:
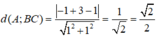
Lời giải:
Gọi giao điểm của $AM$ và $CN$ là $I$
Khi đó $BI$ là đường trung tuyến của tam giác $ABC$ theo tính chất ba đường trung tuyến đồng quy tại một điểm. Theo đó phương trình trung tuyến $BE$ cũng trùng với $BI$
Giao điểm $I$ có tọa độ là nghiệm của HPT:
\(\left\{\begin{matrix} 3x+2y-9=0\\ x-1=0\end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} 3x+2y-9=0\\ x=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3+2y-9=0\\ x=1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} y=3\\ x=1\end{matrix}\right.\)
Vậy $I(1;3)$
Gọi pt đường thẳng $BI$ là $y=ax+b$
Ta có: \(B(-1;3); I(1;3)\in BI\Rightarrow \left\{\begin{matrix} 3=a+b\\ 3=-a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=0\\ b=3\end{matrix}\right.\)
Vậy PT đường trung tuyến là: \(y=3\Leftrightarrow y-3=0\)
b)
Vì \(A\in AM\Rightarrow A(a, \frac{9-3a}{2})\)
Vì \(C\in CN\Rightarrow C(1; c)\)
$I(1;3)$ là trọng tâm của tam giác $ABC$ nên:
\(\left\{\begin{matrix} \frac{x_A+x_B+x_C}{3}=x_I\\ \frac{y_A+y_B+y_C}{3}=y_I\end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} \frac{a+(-1)+1}{3}=1\\ \frac{\frac{9-3a}{2}+3+c}{3}=3\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a=3\\ \frac{\frac{9-3a}{2}+3+c}{3}=3\end{matrix}\right.\) \(\Leftrightarrow \left\{\begin{matrix} a=3\\ \frac{c+3}{3}=3\end{matrix}\right.\Rightarrow a=3; c=6\)
Vậy tọa độ A là: \((3; 0)\), tọa độ C là \((1;6)\)
Os. Htt mình chỉ bảo cho bạn cách lập luận có suy luận
(không lên chỉ biết dựa thụ động vào lý thuyết )
G trọng tâm =>giao CN và AM G(1;3)
BE qua G ; tung độ B và G giống nhau
=> BE//ox qua G => pttq BE ; y-3 =0