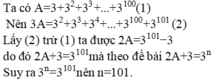Tìm n thuộc N biết A=1+3+32+33+...+310;2.A=3n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
5 tháng 2 2024
Bài 1:
a. $2^{29}< 5^{29}< 5^{39}$
$\Rightarrow A< B$
b.
$B=(3^1+3^2)+(3^3+3^4)+(3^5+3^6)+...+(3^{2009}+3^{2010})$
$=3(1+3)+3^3(1+3)+3^5(1+3)+...+3^{2009}(1+3)$
$=(1+3)(3+3^3+3^5+...+3^{2009})$
$=4(3+3^3+3^5+...+3^{2009})\vdots 4$
Mặt khác:
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+....+(3^{2008}+3^{2009}+3^{2010})$
$=3(1+3+3^2)+3^4(1+3+3^2)+...+3^{2008}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+....+3^{2008})=13(3+3^4+...+3^{2008})\vdots 13$
AH
Akai Haruma
Giáo viên
5 tháng 2 2024
Bài 1:
c.
$A=1-3+3^2-3^3+3^4-...+3^{98}-3^{99}+3^{100}$
$3A=3-3^2+3^3-3^4+3^5-...+3^{99}-3^{100}+3^{101}$
$\Rightarrow A+3A=3^{101}+1$
$\Rightarrow 4A=3^{101}+1$
$\Rightarrow A=\frac{3^{101}+1}{4}$
KV
1 tháng 11 2023
Câu 17
Để n - 1 là ước của 3n + 6 thì (3n + 6) ⋮ (n - 1)
Ta có:
3n + 6 = 3n - 3 + 9 = 3(n - 1) + 9
Để (3n + 6) ⋮ (n - 1) thì 9 ⋮ (n - 1)
⇒ n - 1 ∈ Ư(9) = {-9; -3; -1; 1; 3; 9}
⇒ n ∈ {-8; -2; 0; 2; 4; 10}
Mà n là số tự nhiên
⇒ n ∈ {0; 2; 4; 10}
KV
1 tháng 11 2023
Câu 22
A = 3 + 3² + 3³ + ... + 3²⁰²⁵
⇒ 3A = 3² + 3³ + 3⁴ + ... + 3²⁰²⁶
⇒ 2A = 3A - A
= (3² + 3³ + 3⁴ + ... + 3²⁰²⁶) - (3 + 3² + 3³ + ... + 3²⁰²⁵)
= 3²⁰²⁶ - 3
⇒ 2A + 3 = 3²⁰²⁶ - 3 + 3
⇒ 2A + 3 = 3²⁰²⁶
Mà 2A + 3 = 3ⁿ
⇒ 3ⁿ = 3²⁰²⁶
⇒ n = 2026
OY
20 tháng 7 2021
A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
DX
20 tháng 7 2021
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101
CM
22 tháng 11 2018
Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101
OY
13 tháng 8 2021
A=3+32+33+...+399
3A=32+33+...+3100
3A-A=(32+33+...+3100)-(3+32+33+...+399)
2A=3100-3
2A+3=3100
⇒n=100
BS
13 tháng 8 2021
Đây nè bạn, chúc bạn học tốt :))
A = 3 + 32 + 33+ ... + 399
3A = 3. (3 + 32 + 33+ ... + 399)
3A \(=3^2+3^3+3^4+...+3^{100}\)
3A \(=\left(3^2+3^3+3^4+...+3^{100}\right)-\left(3+3^2+3^3+...+3^{99}\right)\)
2A\(=3^{100}-3\)
Vậy, sau khi tìm đc 2A, ta tìm stn n nha:
2A + 3 = 3n
\(=3^{100}-3+3=3^n\)
⇒\(3^{100}=3^n\)(Vì -3 +3 = 0)
Vậy n = 100
PT
0
BR
3
S
14 tháng 2 2016
, tong từ 1 tới n là 1+2+3+...+n
ta có n/2 căp 1+n = 1+n
2 + (n-1) = 1+n
3 + (n-2) = 1+n
.......
như vậy 1+2+3+4+...+n=(n+1)*n/2
áp dung ta có tong 1+2+3+....+30 = (30+1)*30/2 = 465
như vậy 31 + 32 + 33 +....+ (n-1) +n = (n+1)*n/2 - 465
hay 4585 = (n+1)*n/2 - 465
<=>n^2+n-10100=0
<=>(n-100)(n+101)=0
=>n=100
14 tháng 2 2016
Ta có: 1 + 2+ 3 + ...+ 30 = [30 * ( 30 + 1)] / 2 = 465
==> 31 + 32 + 33 + 34 + ...+ (n-1) + n = [1+ 2+ 3 + ...+ (n-1) + n ] - [1+ 2 + 3 + ...+ 30]
Khi đó ta co: [n* (n+1) ] / 2 - (465) = 4585 ==> [n*(n+1)] / 2 = 5050 ==> n * (n+ 1) = 10100 ==> n^2 + n - 10100 = 0 ==> n^2 + 101n - 100n - 10100 = 0 => n(n+101) - 100( n + 101) = 0 ==> (n-100) * (n+ 101) = 0 ==> n = 100 hoặc n = -101 ( loại)
Vậy n = 100
Câu 2: 6+24+60+96+...+1716
Ta co: 24 + 60 + 96 + ..+ 1716 = 24 + (24 + 1 * 36) + (24 + 2 * 36) + .....+ (24 + 47*36)
Chúng ta thấy số 24 xuất hiện 48 lần
= 24 * 48 + 36 * (1 + 2 + 3 + ...+ 47) = 24 * 48 + 36 * [47*(47+1)/2] = 1152 + 40608 = 41760
vậy kq = 6 + 41760 = 41766
DH
1
H9
HT.Phong (9A5)
CTVHS
5 tháng 7 2023
\(A=3+3^2+3^3+...+3^{2015}\)
\(\Rightarrow3A=3^2+3^3+...+3^{2015}+3^{2016}\)
\(\Rightarrow3A-A=\left(3^2+3^3+...+3^{2016}\right)-\left(3+3^2+3^3+...+3^{2015}\right)\)
\(\Rightarrow2A=\left(3^2-3^2\right)+\left(3^3-3^3\right)+...+\left(3^{2016}-3\right)\)
\(\Rightarrow2A=3^{2016}-3\)
\(\Rightarrow A=\dfrac{3^{2016}-3}{2}\)
Ta có: \(2A+3=3^n\)
\(\Rightarrow2\cdot\dfrac{3^{2016}-3}{2}+3=3^n\)
\(\Rightarrow3^{2016}-3+3=3^n\)
\(\Rightarrow3^{2016}=3^n\)
\(\Rightarrow n=2016\)