Cho ba điểm M(2;0); N(-1;3) P(-2;2). Điểm E thuộc đường tròn (C) : \(\left(x+1\right)^2+\left(x-4\right)^2=25\). Tìm giá trị nhỏ nhất của \(\left|\overrightarrow{EM}+2\overrightarrow{EN}+3\overrightarrow{EP}\right|\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2016
B nằm giữa hai điểm còn lại; vì đây là 2tia đối nhau
Tích nhá!hi
CM
30 tháng 11 2018
Chọn B.
Ta có M nằm trên trục Oy nên tọa độ điểm M có dạng M(0; y)
Ba điểm A; B; M thẳng hàng khi 
cùng phương với 
Ta có 
. Do đó, 
cùng phương với
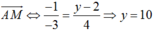
Vậy M(0; 10) .
CM
3 tháng 5 2019
Ta có P ∈ O x nên P( x; 0) và M P → = x + 2 ; − 2 M N → = 3 ; − 1 .
Do M, N, P thẳng hàng nên 2 vecto M P → ; M N → cùng phương
⇒ x + 2 3 = − 2 − 1 = 2 ⇔ x + 2 = 6 ⇔ x = 4 ⇒ P 4 ; 0 .
Chọn D.
CM
13 tháng 1 2017
Ta có P ∈ O x nên P(x; 0) và M P → = x + 2 ; − 2 M N → = 3 ; − 1 .
Do M, N, P thẳng hàng nên x + 2 3 = − 2 − 1 ⇔ x = 4 ⇒ P 4 ; 0 .
Chọn D.