Cho hình vuông ABCD biết A(0;2), BC: x -2y-1=0 và điểm C có hoành độ dương. Tìm tọa độ tâm N của hình vuông ABCD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a)` Vì `5xx5=25` nên cạnh hình vuông bằng `5 cm`
Bán kính hình tròn là: `5:2=2,5(cm)`
Diện tích hình tròn là: `2,5xx2,5xx3,14=19,625(cm^2)`
`b)` Vì `2\sqrt{3}xx2\sqrt{3}=12` nên cạnh hình vuông bằng `2\sqrt{2} cm`
Bán kính hình tròn là: `2\sqrt{3}:2=\sqrt{3})(cm)`
Diện tích hình tròn là: `\sqrt{3}xx\sqrt{3}xx3,14=9,42(cm^2)`
Diện tích phần gạch chéo là: `12-9,42=2,58(cm^2)`

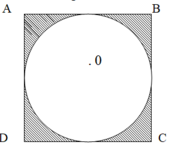
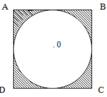
a. Từ hình vẽ, ta thấy cạnh của hình vuông B bằng đường kính của hình tròn - do đó ta có:
|
( R x 2 ) x ( R x 2 ) = 25
R x 2 x R x 2 = 25
R x R x 4 = 25
R x R = 25 : 4 = 6,25
Vậy diện tích hình tròn là: 6,25 x 3,14 = 19,625 ( c m 2 )
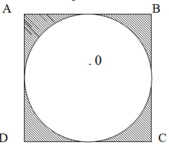
b, Vì ( R x 2 ) x ( R x 2 ) = 12
R x R x 4 = 12
R x R = 12 : 4 = 3
Vậy diện tích phần gạch chéo là: 3 x 3,14 : 4 = 0,645 ( c m 2 )
Đáp số: 19,625 c m 2
0,645 c m 2

B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
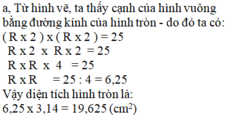



Do ABCD là hình vuông \(\Rightarrow AB=d\left(A;BC\right)=\dfrac{\left|0-2.2-1\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{5}\)
\(\Rightarrow AC=AB\sqrt{2}=\sqrt{10}\)
Do C thuộc BC \(\Rightarrow C\left(2c+1;c\right)\) \(\Rightarrow\overrightarrow{AC}=\left(2c+1;c-2\right)\)
\(\Rightarrow AC^2=\left(2c+1\right)^2+\left(c-2\right)^2=10\)
\(\Leftrightarrow5c^2-5=0\Rightarrow\left[{}\begin{matrix}c=1\\c=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}C\left(3;1\right)\\C\left(-1;-1\right)\end{matrix}\right.\)
Do C có hoành độ dương \(\Rightarrow C\left(3;1\right)\)
N là trung điểm AC \(\Rightarrow N\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)