chứng minh với mọi STN a khác 0 ta luôn có UCLN(a;15).3=UCLN(3a;45)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 7 2018
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
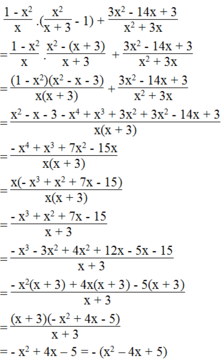
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
A
1
2 tháng 9 2021
\(x^2-3xy+6y^2\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}y+\dfrac{9}{4}y^2+\dfrac{15}{4}y^2\)
\(=\left(x-\dfrac{3}{2}y\right)^2+\dfrac{15}{4}y^2>0\forall x,y\)
4 tháng 10 2023
Bước 1: Chứng minh công thức đúng cho n = 1. Khi n = 1, ta có: 1² = 1 = 1 . (1 + 1) . (2 . 1 + 1) / 6 = 1. Vậy công thức đúng cho n = 1.
Bước 2: Giả sử công thức đúng cho n = k, tức là 1² + 2² + ... + k² = k . (k + 1) . (2k + 1) / 6. Ta cần chứng minh công thức đúng cho n = k + 1, tức là 1² + 2² + ... + k² + (k + 1)² = (k + 1) . (k + 1 + 1) . (2(k + 1) + 1) / 6.
Bước 3: Chứng minh công thức đúng cho n = k + 1. Ta có: 1² + 2² + ... + k² + (k + 1)² = (k . (k + 1) . (2k + 1) / 6) + (k + 1)² = (k . (k + 1) . (2k + 1) + 6(k + 1)²) / 6 = (k . (k + 1) . (2k + 1) + 6(k + 1) . (k + 1)) / 6 = (k + 1) . ((k . (2k + 1) + 6(k + 1)) / 6) = (k + 1) . ((2k² + k + 6k + 6) / 6) = (k + 1) . ((2k² + 7k + 6) / 6) = (k + 1) . ((k + 2) . (2k + 3) / 6) = (k + 1) . ((k + 1 + 1) . (2(k + 1) + 1) / 6).
Vậy, công thức đã được chứng minh đúng cho mọi số tự nhiên n khác 0.
CM
5 tháng 7 2018
Điều kiện x ≠ 1 và x ≠ - 1
Ta có:
Biểu thức dương khi x 2 + 2 x + 3 > 0
Ta có: x 2 + 2 x + 3 = x 2 + 2 x + 1 + 2 = x + 1 2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1
9 tháng 11 2015
a)7a=11b
7=11b:a
7:11=b:a
Theo yêu cầu ban đầu thì a=11; b=7
Còn theo yêu cầu sau cùng là ƯCLN(a;b)=45 thì ta chỉ cần nhân cho 45 nữa là xong ngay: a=11.45=495; b=7.45=315
VẬY: a=495; b=315
Còn bài thứ 2 thì dễ ẹt, cứ tìm 1 số a bất kì, rồi tìm số b bằng cách lấy \(a^2\), rồi tìm số c bằng cách lấy \(a^3\)
VD: a=2 thì b=\(a^2\)=4 và c=\(a^3\)=8
a.b=8 chia hết cho c, b.c=32 chia hết cho a, a.c=16 chia hết cho b
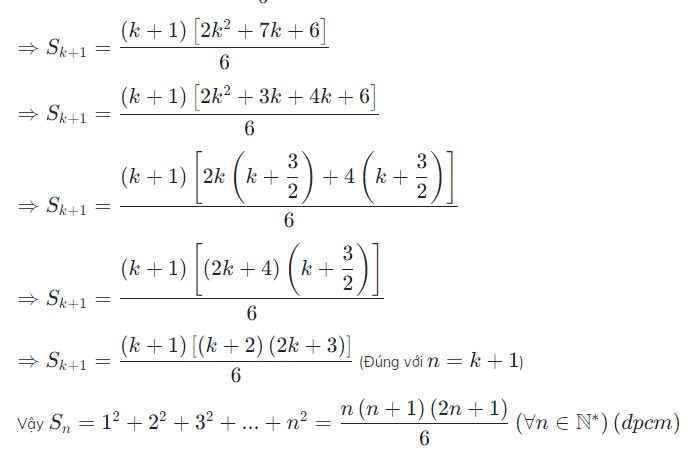
CAOIUYIVFVBNGHNVYI