.Cho tam giác ABC vuông tại A. gọi H là hình chiếu của A lên BC, M(2;-1) trung điểm HB,N trung điểm HC. K(-1/2;1/2) là trực tâm tam giác AMN. Tìm C, biết yA<0, A thuộc d:x+2y+4=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC vuông góc SA
BC vuôg góc AB
=>BC vuông góc (SAB)
b: BI vuông góc SA
BI vuông góc AC
=>BI vuông góc (SAC)

Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC

a: Xét ΔABC vuông tại A có sin C=AB/BC=3/5
=>cos C=căn 1-(3/5)^2=4/5
=>AC/BC=4/5
=>BC=20(cm)
\(AB=\sqrt{20^2-16^2}=12\left(cm\right)\)
ΔABC vuông tại A có AH là đường cao
nên CH*CB=CA^2
=>CH*20=16^2=256
=>CH=12,8(cm)
b: ΔHAB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔHAC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN đồng dạng với ΔACB

Xét ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
Xét ΔAHC vuông tại H có HD là đường cao
nên AD*AC=AH^2
=>AE*AB=AD*AC
=>AE/AC=AD/AB
mà góc DAE chung
nên ΔAED đồng dạng với ΔACB

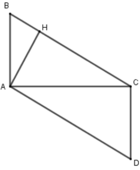
Xét ΔABC và ΔCDA có:
AB = CD (t/c)
AC chung
BAC = DCA = 90 ∘
Suy ra ΔABC = ΔCDA (c-g-c) nên D đúng.
Ta có: S A B C = 1 2 AH.BC = 1 2 AB.AC => AH.BC = AB.AC ⇒ A H A B = A C B C
Xét ΔABC và ΔHAC có:
CAH = ABC (cùng phụ góc C)
A H A B = A C B C (cmt)
Suy ra ΔABC ~ ΔHAC (c - g - c) nên A sai
Ngoài ra, ΔADC = ΔCBA và ΔCBA ~ ΔCAH hay ΔADC ~ ΔCAH nên B đúng
Từ A H A B = A C B C ⇒ A H B C = A B B C
Xét ΔABH và ΔCBA có:
Chung B
=> ΔABH ~ ΔCBA (c-g-c)
Mà ΔADC = ΔCBA nên ΔABH ~ ΔADC hay C đúng
Vậy chỉ có A sai.
Đáp án: A

c: Xét ΔAHB vuông tại H có \(cosB=\dfrac{BH}{BA}\)
Xét ΔHMB vuông tại M có \(cosB=\dfrac{MB}{BH}\)
Xét ΔABC vuông tại A có \(\left\{{}\begin{matrix}cosB=\dfrac{BA}{BC}\\cosC=\dfrac{AC}{BC}\end{matrix}\right.\)
Xét ΔCKH vuông tại K có \(cosC=\dfrac{CK}{CH}\)
Xét ΔCHA vuông tại H có \(cosC=\dfrac{CH}{CA}\)
\(cos^3C=cosC\cdot cosC\cdot cosC\)
\(=\dfrac{CA}{CB}\cdot\dfrac{CK}{CH}\cdot\dfrac{CH}{CA}=\dfrac{CK}{CB}\)
=>\(CK=CB\cdot cos^3C\)
\(cos^3B=cosB\cdot cosB\cdot cosB\)
\(=\dfrac{BH}{BA}\cdot\dfrac{MB}{BH}\cdot\dfrac{BA}{BC}=\dfrac{MB}{BC}\)
=>\(MB=BC\cdot cos^3B\)
\(BM+CK\)
\(=BC\cdot cos^3B+BC\cdot cos^3C\)
\(=BC\left(cos^3B+cos^3C\right)\)