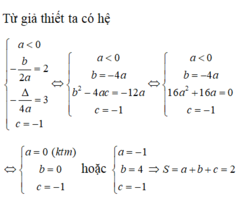Biết rằng (P):y= a x 2 bx c, đi qua điểm A(1;10) và có đỉnh I(-2;1). Tính tổng S= 7 a 2 27 b 2 - 2021 c 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 10 2020
a/ Ta có hệ điều kiện:
\(\left\{{}\begin{matrix}-\frac{b}{2a}=2\\\frac{4ac-b^2}{4a}=4\\c=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\24a-b^2=16a\\c=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\8a-16a^2=0\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=-2\\c=6\end{matrix}\right.\) \(\Rightarrow P\)
b/ \(\left\{{}\begin{matrix}-\frac{b}{2a}=2\\\frac{4ac-b^2}{4a}=3\\c=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\-4a-b^2=12a\\c=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\16a^2+16a=0\\c=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=4\\c=-1\end{matrix}\right.\) \(\Rightarrow S\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Do (P) qua A;B;C, thay tọa độ A, B, C vào pt (P) ta được:
\(\left\{{}\begin{matrix}a+b+c=-1\\4a+2b+c=3\\a-b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\\c=-3\end{matrix}\right.\)
\(\Rightarrow\left(P\right):\) \(y=x^2+x-3\)
23 tháng 10 2020
parabol y= ax2+bx+c đi qua A(2,-7)
\(\Rightarrow-7=a.2^2+b.2+c\)
\(\Rightarrow-7=4a+2b+c\)
\(\Rightarrow4a+2b+c=-7\)(1)
parabol y=ax2+bx+c đi qua B (-5,0)
\(\Rightarrow0=a\left(-5\right)^2+b.\left(-5\right)+c\)
\(\Rightarrow0=25a-5b+c\)
\(\Rightarrow25a-5b+c=0\)(2)
parabol có trục đối cứng là x=2 nên ta có
\(\frac{-b}{2a}=2\Leftrightarrow-b=4a\Leftrightarrow4a+b=0\left(3\right)\)
từ (1) ,(2) và (3) ta có hệ phương trình
\(\left\{{}\begin{matrix}4a+2b+c=-7\\25a-5b+c=0\\4a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\frac{1}{7}\\b=\frac{-4}{7}\\c=\frac{-45}{7}\end{matrix}\right.\)
đây là theo cách mình làm thôi k hắc là đúng hya sai đâu cho dù sai bạn cũng dựa vào cái kiểu này mà tính nhé
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua điểm A(8; 0) nên:
\(a{.8^2} + b.8 + c = 0 \Leftrightarrow 64a + 8b + c = 0\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh là I(6;-12):
\(\frac{{ - b}}{{2a}} = 6 \Leftrightarrow - b = 12a \Leftrightarrow 12a + b = 0\)
\(a{.6^2} + 6b + c = - 12 \Leftrightarrow 36a + 6b + c = - 12\)
Từ 3 phương trình trên ta có: \(a = 3;b = - 36,c = 96\)
=> Hàm số cần tìm là \(y = 3{x^2} - 36x + 96\)
6 tháng 3 2023
\(\left(P\right):y=ax^2+bx+2\)
Vì (P) đi qua điểm \(M\left(1;5\right)\) nên ta có: \(a.1^2+b.1+2=5\Leftrightarrow a+b=3\) (1)
Mà (P) có trục đối xứng là \(x=\dfrac{-1}{4}\) nên: \(\dfrac{-b}{2a}=\dfrac{-1}{4}\)
\(\Leftrightarrow-2a=-4b\Leftrightarrow-2a+4b=0\) (2)
Từ (1) và (2) ta có:
\(\left\{{}\begin{matrix}a+b=3\\-2a+4b=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
Vậy parabol cần tìm có dạng: \(y=2x^2=x+2\)
6 tháng 3 2023
xác định parabol (p): y= ax^2+2x+c biết rằng i (1/2; 11/2) là đỉnh của (p)
giải dùm t câu này vs c
CM
7 tháng 2 2017
Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13
13 tháng 12 2021
\(\Leftrightarrow\left\{{}\begin{matrix}1+b+c=0\\4-2b+c=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b+c=-1\\c-2b=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{11}{3}\\c=\dfrac{8}{3}\end{matrix}\right.\\ \Leftrightarrow\left(P\right):y=x^2-\dfrac{11}{3}x+\dfrac{8}{3}\)
